Osservate la figura qui sotto e, in particolare, i quattro triangoli colorati:
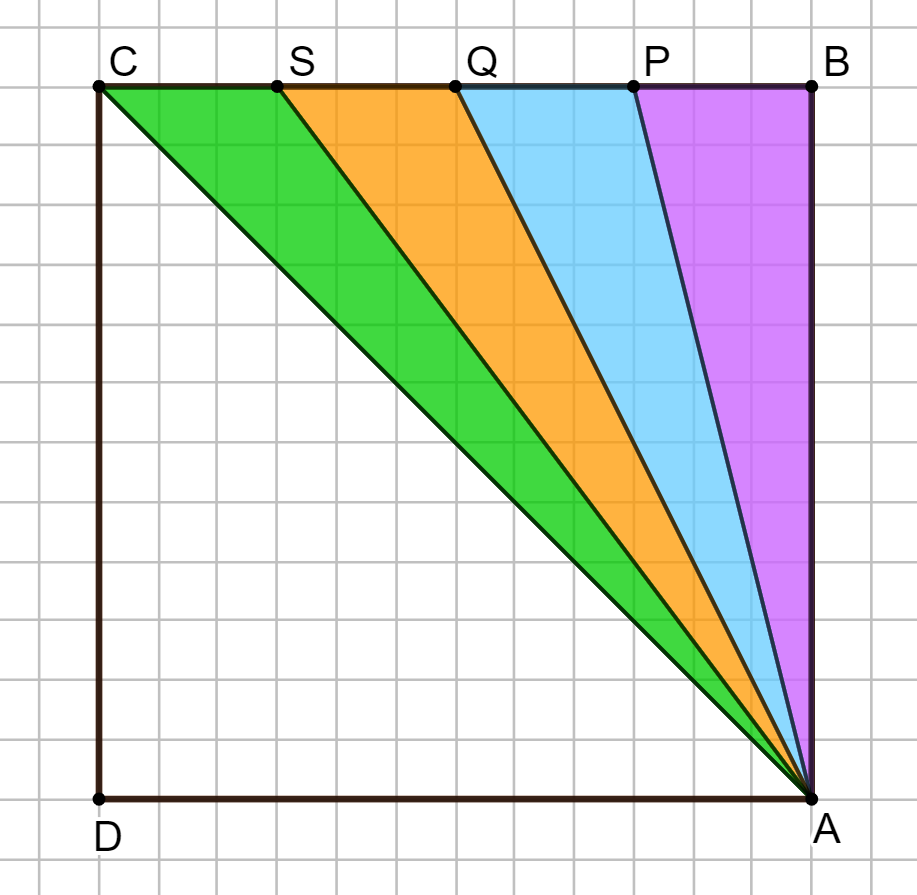
Leggi tutto “Quanto sono grandi questi triangoli?”
Multipli e divisori
12 è multiplo di 6 e 20 è multiplo di 4.
Il prodotto 12·20=240 è multiplo di 8.
È sempre vero che, se a è multiplo di 6 e b è multiplo di 4, allora il prodotto a·b è multiplo di 8?
Se non è vero, date l’esempio di due numeri a e b per cui questo non succede; se è sempre vero, spiegate perché ne siete convinti.
Leggi tutto “Multipli e divisori”
Allegati
Multipli e divisori, pari e dispari
Considerate i divisori di 15: sono tutti pari? Sono tutti dispari? O alcuni sono pari e altri sono dispari?
Considerate i divisori di 2000: sono tutti pari? Sono tutti dispari? O alcuni sono pari e altri sono dispari?
Leggi tutto “Multipli e divisori, pari e dispari”
Allegati
Nel castello di Re Infinito
Un giorno, Bernardo, Giorgio e Riccardo riuscirono a entrare di nascosto nel cortile del castello di Re Infinito. Il loro sguardo fu subito attratto da due scatole ben sigillate, una color rosso rubino e l’altra color verde smeraldo.
Leggi tutto “Nel castello di Re Infinito”
Allegati
Un gioco con i dadi
Vi proponiamo un gioco da fare a coppie.
Servono due dadi e due tabelle (una per ciascun giocatore) con i numeri da 1 a 12, ciascuno ripetuto due volte.
Ogni turno consiste nel tiro dei due dadi, simultaneamente, da parte di un giocatore.
Al proprio turno il giocatore può cancellare dalla propria tabella, in alternativa, o i due numeri usciti o il numero che è somma dei due numeri usciti.
Leggi tutto “Un gioco con i dadi”
Allegati
Biancaneve e i 77 funghi
Biancaneve divide tra i sette nani il suo raccolto di 77 funghi.
Comincia a servire il più piccolo, Cucciolo, e poi di seguito serve tutti gli altri: Mammolo, Brontolo, Eolo, Dotto, Gongolo e Pisolo.
Ogni nano riceve un fungo in più di quello che l’ha immediatamente preceduto e Biancaneve riesce così a distribuire tutti i funghi raccolti.
Leggi tutto “Biancaneve e i 77 funghi”
Allegati
Le confezioni della BestEraser
Per condividere con gli alunni il video che presenta questo problema, fornire il seguente link:
https://youtu.be/R5FFWDh5GoE
Domande e risposte
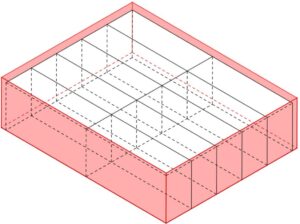
La gomma per cancellare descritta nel video-problema è un parallelepipedo i cui spigoli misurano 3,5 cm, 1,8 cm e 1,1 cm.
La ditta che produce queste gomme vuole imballarle in confezioni da dieci gomme ciascuna e sta valutando la possibilità di usare delle scatole già disponibili a magazzino: le scatole rosse (parallelepipedi di dimensioni 7,2 cm, 5,7 cm e 1,9 cm), le scatole blu (parallelepipedi di dimensioni 12 cm, 6,5 cm e 1,5 cm) o le scatole gialle (parallelepipedi di dimensioni 7,4 cm, 3,5 cm e 2,5 cm).
Ai ragazzi si chiede, in particolare, se c’è qualche scatola in cui si riescono a sistemare 10 gomme. Viene anche chiesto di descrivere il procedimento utilizzato per rispondere.
Per cominciare, si può calcolare il volume di una gomma e delle diverse scatole:
- il volume di una gomma è 3,5 cm x 1,8 cm x 1,1 cm = 6,93 cm3 (quindi il volume di 10 gomme è 69,3 cm3);
- il volume della scatola rossa è 7,2 cm x 5,7 cm x 1,9 cm = 77,976 cm3;
- il volume della scatola blu è 12 cm x 6,5 cm x 1,5 cm = 117 cm3;
- il volume della scatola gialla è 7,4 cm x 3,5 cm x 2,5 cm = 64,75 cm3.
In base a questi calcoli si può essere certi che la scatola gialla non riesce a contenere 10 gomme, dato che 64,75 < 69,3.
Non è però possibile, solo dal confronto dei volumi, stabilire molto altro. In particolare, il fatto che il volume della scatola rossa e quello della scatola blu siano maggiori del volume occupato da 10 gomme non basta per poter dire che queste scatole possano contenere 10 gomme, perché le gomme non sono un fluido che può essere versato nella confezione assumendone la forma!
La scatola rossa può contenere effettivamente 10 gomme: possiamo disporle in due file da 5 gomme ciascuna in modo che il lato da 1,8 cm della gomma sia in verticale (e possiamo farlo perché l’altezza della scatola è 1,9 cm e 1,8<1,9). Il fatto che 5×1,1<5,7 ci garantisce che lungo il lato da 5,7 cm ci stanno i lati da 1,1 cm di 5 gomme; il fatto che 2×3,5<7,2 ci garantisce che lungo il lato da 7,2 cm ci stanno i lati da 3,5 cm di 2 gomme.
Per quanto il volume della scatola blu sia ancora più grande di quello della scatola rossa, la scatola blu non può contenere 10 gomme. L’altezza della scatola (1,5 cm) infatti rende obbligatorio disporre le gomme in modo che il lato da 1,1 cm sia in verticale (gli altri lati della gomma infatti sono entrambi più lunghi di 1,5 cm). Con qualche tentativo, non è difficile rendersi conto che più di 9 gomme non possono essere inserite nella scatola blu.
Commenti
L’idea per Le confezioni della BestEraser è nata dalla discussione sorta tra alcuni insegnanti in merito a questo problema (tratto da un sussidiario per la scuola primaria):
Per alcuni degli insegnanti che hanno partecipato alla discussione, il problema così posto non poteva essere risolto, perché nulla si dice sulla forma delle scatole; altri giungevano alla stessa conclusione, dando però per scontato che le scatole fossero dei parallelepipedi e lamentando il fatto di non conoscerne le dimensioni; altri ancora calcolavano il volume della cassa cubica (48 cm x 48 cm x 48 cm = 110592 cm3) e lo dividevano per il volume della singola scatola (110592 cm3 : 96 cm3 = 1152).
È bastato poco, tra colleghi, per trovare quale errore e quale “pregiudizio” si nascondesse sotto la sicurezza di chi sosteneva che nella cassa si potessero inserire 1152 scatole, indipendentemente dalla loro forma; è bastato chiudere gli occhi e cercare di immaginarsi la situazione, per capire che se le scatole da inserire sono sferiche o cilindriche, o hanno forme poliedriche ma bislacche, si “perde” un sacco di spazio. La discussione è proseguita poi per cercare di costruire per gli alunni un problema con un testo meno “perentorio”, che di per sé li invitasse a discutere e a non dare troppe cose per scontate.
Un problema significativo
Quanto raccontato nel video-problema non è un puro espediente, ma corrisponde a un problema reale, che si pone spesso a coloro che si occupano di attività produttive e commerciali: quello di impacchettare un certo numero di prodotti in una confezione oppure di ottimizzare la maniera di caricare in un camion un certo numero di scatole, magari anche di forme e dimensioni diverse.
I problemi di impacchettamento possono diventare davvero difficili, ma anche questo – nella sua relativa semplicità – è significativo perché fa capire come non sia sufficiente ragionare col volume degli oggetti e del contenitore in questione (nel nostro caso le gomme e le scatole), ma è necessario tenere conto della loro forma e dei differenti modi per disporre gli oggetti nel contenitore.
Se avessimo a che fare con fialette contenenti 6,93 cm3 di un certo liquido e volessimo riversare questo liquido in una bottiglietta della capacità di 117 cm3, basterebbe calcolare 117:6,93 per sapere che potremmo svuotare nella bottiglietta più di 16 ma meno di 17 fialette. Però se 6,93 cm3 è il volume di una gomma e 117 cm3 quello di una scatola, il risultato di questa divisione non ci dice molto.
Il volume ci dà effettivamente delle informazioni. E possono anche essere informazioni che tagliano la testa al toro in modo molto comodo: per esempio, è bastato calcolare il volume della scatolina gialla per dire che essa non può contenere 10 gomme (perché il suo volume è minore di quello di 10 gomme). In generale, il fatto che una scatola abbia il volume maggiore del volume di 10 gomme è una condizione necessaria affinché la scatola contenga 10 gomme.
Non è però una condizione sufficiente. Lo si può capire facilmente pensando ad una scatola anche dal volume enorme, con due dimensioni enormi, ma con la terza dimensione minore di 1 cm (e quindi più corta dello spigolo più piccolo della gomma, lungo 1,1 cm): in una scatola di questo tipo, per quanto il suo volume possa essere arbitrariamente grande, non si riesce a infilare nemmeno una gomma!
Da questa osservazione è possibile ricavare una condizione sufficiente (ma non necessaria) affinché si possano inserire 10 gomme in una scatola: se una delle dimensioni della scatola è (anche di poco) più grande di una delle dimensioni della gomma moltiplicata per 10, basta che ciascuna delle altre due dimensioni della scatola sia (anche di poco) più grande di una delle altre due dimensioni della gomma; in questo caso le gomme si potranno inserire nella scatola in una unica fila formata da 10 gomme.
Un’altra condizione sufficiente (ma, ancora, non necessaria) affinché si possano inserire 10 gomme in una scatola potrebbe essere questa: se una delle dimensioni della scatola è (anche di poco) più grande di una delle dimensioni della gomma moltiplicata per 5, e un’altra dimensione della scatola è (anche di poco) più grande del doppio di un’altra dimensione della gomma, basta che la terza dimensione della scatola sia (anche di poco) più grande della terza dimensione della gomma; in questo caso le gomme si potranno inserire nella scatola in due file sovrapposte formate da 5 gomme ciascuna.
Queste condizioni sono facili da verificare con i conti o con il righello (che misura lunghezze e non volumi!) come suggerito nel video, anche senza costruire in cartoncino 10 modellini di gomme: conti o righello possono essere utilizzati per controllare quante volte le dimensioni della gomma siano contenute in quelle delle scatoline, focalizzando l’attenzione sulle dimensioni lineari.
Chiaramente nessuna di queste due condizioni è necessaria, dal momento che non si richiede che tutte le gomme siano riposte “nello stesso modo” all’interno della scatola. Con questo intendiamo dire che, per quanto quelle di questo tipo siano le disposizioni con le quali ci viene più “naturale” fare i primi tentativi, non è detto che gli spigoli delle gomme di uguale lunghezza debbano essere tutti paralleli e quindi molte altre disposizioni sono possibili.
Strategie risolutive diverse
Possiamo prevedere, accettare e addirittura stimolare sia un approccio molto concreto a questo problema (quello di chi costruisce i modellini in cartoncino e va per tentativi) sia un approccio più astratto (quello di chi si mette a ragionare direttamente sulle misure).
Se in una classe gruppi di alunni diversi useranno diversi approcci, confrontarli durante la discussione finale sarà un arricchimento per tutti.
Potrebbero inoltre emergere modi diversi di sistemare lo stesso numero di gomme all’interno della stessa scatola. Anche questa molteplicità di proposte sarà da valorizzare: spesso abbiamo (e più noi adulti dei ragazzi…!) un modo di pensare molto rigido e stereotipato per cui, se siamo abituati a vedere la gomma appoggiata al tavolo in un certo modo, tendiamo a pensarla solo in quella posizione anche quando dobbiamo immaginare come riporla nella scatola. Se qualche gruppo non riuscisse a inserire 10 gomme nella scatola rossa, ciò potrebbe essere dovuto proprio al continuare a pensare alle gomme appoggiate al fondo della scatola sulla loro faccia “più estesa”: vedere le 10 gomme inscatolate dai loro compagni potrà aiutarli a superare questa rigidità.
Un problema aperto
Sono tante le domande che potrebbero nascere nei ragazzi, o che l’insegnante potrebbe porre loro per continuare a riflettere sui nodi proposti da questo problema o per verificarne l’effettiva comprensione. Ad esempio:
- sapreste progettare altre scatole a forma di parallelepipedo, che contengano 10 gomme uguali a quelle descritte nel video-problema?
- sapreste immaginare una scatola a forma di parallelepipedo, con un volume maggiore di quello di 10 gomme (cioè un volume maggiore di 69,3 cm3), dove però non si riesca a far stare nemmeno una gomma di quelle descritte nel video-problema?
- sapreste immaginare una gomma, sempre a forma di parallelepipedo, sempre con un volume di 6,93 cm3 che però, anche da sola, non possa essere contenuta in alcuna delle tre scatole descritte nel video-problema?
Scenari possibili
Questo video-problema può essere tranquillamente proposto in una classe terza della scuola secondaria di primo grado.
Ma può essere proposto pure in una classe quinta della scuola primaria, anche senza dover dare a ciascun gruppo di lavoro le dieci gomme e le tre scatoline, a patto di averli fatti lavorare in precedenza su alcuni esempi concreti: quante risme di carta ci stanno nel cassetto della cattedra? Quante scatole di un certo tipo ci stanno nell’armadio della classe? Quanti volumi dell’enciclopedia ci stanno nello scaffale della libreria della biblioteca? Quanti pacchetti di fazzolettini di carta ci stanno nella scatola che la maestra ha portato per tenerli in classe?
Materiale necessario
Come già specificato, non è necessario che ogni gruppo di lavoro abbia a disposizione le tre scatole e le 10 gomme, anzi: il fatto di non averle (o di essere sufficientemente pigri per non aver voglia di costruirsene dei modelli in cartoncino) può spronare verso il ragionamento e l’astrazione.
È però importante che venga lasciata la possibilità a chi ne sente l’esigenza di costruirsi questi modelli in cartoncino, in modo da verificare le proprie ipotesi o da avere abbastanza elementi per formularne di nuove.
Un modello concreto costruito dall’insegnante, o le foto riportate in questo articolo, o alcuni disegni ben fatti possono essere d’aiuto per convincere alunni particolarmente scettici e particolarmente in difficoltà.
Problemi collegati
Tra i Problemi per matematici in erba ce n’è un altro, sempre legato a come alcuni parallelepipedi possano essere inscatolati in un parallelepipedo più grande: La fabbrica di saponette.
I due problemi, per quanto simili, offrono spunti di riflessione diversi e complementari.
Un prisma stellare
Giovanna, come compito per casa, deve trovare il volume di un prisma che ha questa forma:
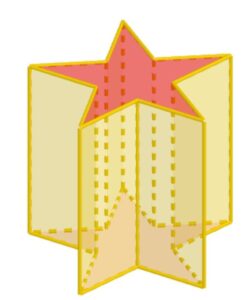
Sa che la base è una stella regolare a cinque punte i cui lati misurano tutti 2 cm e sa che il prisma è alto 5 cm. Però non ha la più pallida idea di come calcolare l’area della stella.
Leggi tutto “Un prisma stellare”
Allegati
Prismi, piramidi e altro
Questo è un problema che potreste esplorare anche a occhi chiusi, cercando di esercitare la vostra fantasia, e discutendo fra di voi in modo da usare l’immaginazione di tutti. Pensiamo però che a un certo punto vi sarà utile aprire gli occhi e provare a costruire qualche oggetto.
Leggi tutto “Prismi, piramidi e altro”
Allegati
Costruire un pallone da calcio
Per condividere con gli alunni il video che presenta questo problema, fornire il seguente link:
https://youtu.be/lNfwicOaAHs
Domande e risposte
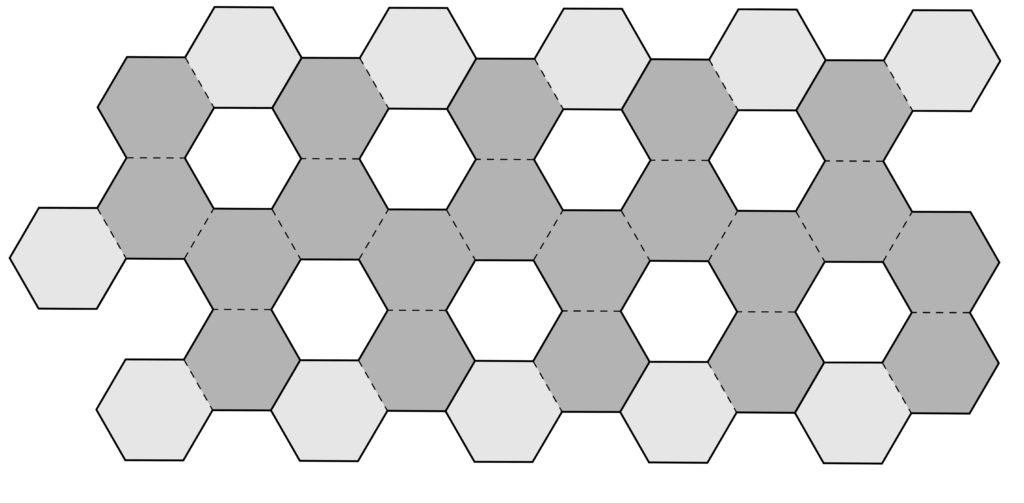
A partire dal reticolo esagonale allegato a fondo pagina (citato nel video come “il disegno di Simone”) è possibile costruire un solido che ricorda un pallone da calcio.
Quante facce esagonali ha questo solido? E quante pentagonali?
Il solido che si ottiene nel video e che assomiglia a un pallone da calcio ha 20 facce esagonali e 12 “buchi” pentagonali, in corrispondenza di ciascuno dei quali possiamo immaginare una faccia.
Quanti esagoni ci sono nel reticolo del disegno di Simone?
Nel reticolo che appare sul disegno mostrato nel video si possono contare 39 esagoni, 8 dei quali vengono poi “eliminati” dai tagli lungo le linee continue.
Istruzioni
La richiesta di scrivere delle istruzioni precise, che consentano a chi non ha visto il video di ricostruire il solido, può essere soddisfatta in molti modi.
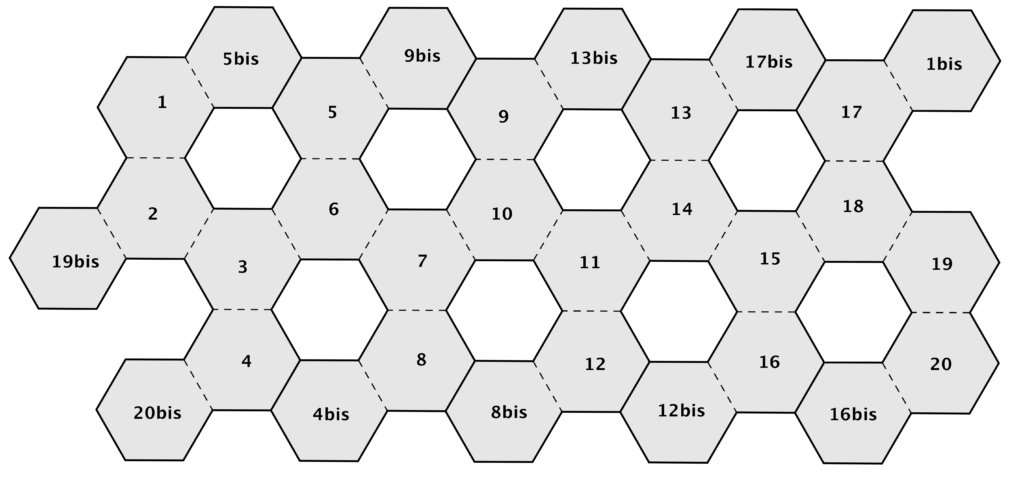
Dalle istruzioni deve emergere il fatto che alcuni esagoni vanno incollati su altri esagoni, lasciando dei “buchi” a forma di pentagono. Come suggerito nel video, indicare sullo stesso disegno quali esagoni vadano incollati su quali altri potrebbe facilitare di molto le cose.
Commenti
Un problema significativo
Immaginare a occhi chiusi, costruire a occhi aperti
Spesso, nella scuola, si parla della necessità di sviluppare le capacità di visualizzazione spaziale degli alunni. Particolarmente rilevante è, a questo proposito, la capacità di pensare il solido che si può costruire a partire da un certo sviluppo piano. Questa abilità può essere allenata attraverso varie esperienze concrete, purché sempre accompagnate da opportune riflessioni: costruire solidi a partire dal loro sviluppo piano; disegnare lo sviluppo piano di un solido dato; individuare sviluppi piani diversi dello stesso solido; indicare – su un dato sviluppo – quali lati dei poligoni che lo compongono andranno a combaciare con quali altri lati per costruire un certo solido…
In questo problema, le abilità di visualizzazione spaziale degli alunni entrano ancor più in gioco, insieme alla immaginazione, in quanto il reticolo esagonale disegnato sul foglio di carta NON coincide con lo sviluppo piano del solido: ci sono tanti esagoni di troppo e… mancano i pentagoni!
Dove si nascondono alcuni esagoni? Da dove vengono i pentagoni? Nello scrivere le istruzioni richieste, gli alunni dovranno, in un certo senso, rispondere a queste domande.
La situazione che si presenta più frequentemente è questa: 6 esagoni disposti ad anello attorno a un settimo esagono completamente delimitato da linee continue (e che quindi diventerà un buco nel reticolo); i 6 esagoni diventano 5 perché uno di essi viene incollato su un altro e l’esagono centrale diventa un buco pentagonale.
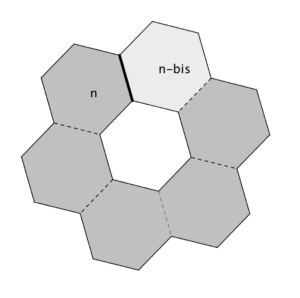
Ma ci sono anche coppie di esagoni che sul reticolo sono “lontani” e che devono essere incollati uno sull’altro: lo si capisce anche prima di aver costruito il solido, perché altrimenti non si potrebbe ottenere qualcosa che assomiglia a un pallone. Non è però facile capire di quali esagoni si tratti, se ci si limita a osservare il reticolo o a guardare il video! Dopo aver costruito il solido, però, attraverso un gioco di passaggi continui dalla manipolazione alla riflessione (e viceversa), dal pensare al toccare (e viceversa), dal costruire a occhi aperti all’immaginare a occhi chiusi (e viceversa) i ragazzi potranno concludere che gli esagoni “lontani” da incollare uno sull’altro saranno quelli indicati in FIGURA 2 con le etichette 1 e 1bis, 19 e 19bis, 20 e 20bis.
cogliere le analogie
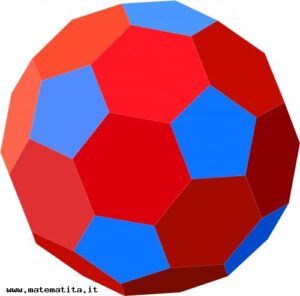
Una buona dose di immaginazione serve anche per vedere l’analogia tra il pallone da calcio e l’oggetto, pieno di buchi, che si costruisce col cartoncino, nonché tra questo oggetto e il poliedro archimedeo con 20 facce esagonali e 12 facce pentagonali che è rappresentato nella figura qui sotto.
Un problema memorabile
Tanti fattori possono rendere questo problema memorabile: lo stupore che si prova nel vedere che da un reticolo fatto di soli esagoni nasce un solido in cui si individuano anche dei pentagoni, il fatto che si parli di un oggetto tanto comune quanto amato come il pallone da calcio, il fatto che i ragazzi si scoprano capaci di costruire da soli qualcosa di veramente bello…
Ciascun insegnante, nel contesto della propria classe, saprà agganciare a questo problema discussioni, riflessioni e scoperte in modo tale che tornino facilmente alla mente degli alunni, ogni volta che rivedranno o ripenseranno a un pallone da calcio!
Un problema aperto
In questo video-problema si chiede agli alunni di contare quanti sono gli esagoni e quanti sono i buchi pentagonali nell’oggetto che si costruisce a partire dal reticolo esagonale, che è come contare gli esagoni e i pentagoni che, una volta cuciti insieme, formano un pallone da calcio; ed è anche come contare le facce del poliedro che il pallone da calcio richiama.
È probabile che, mentre cercano di risolvere questo problema, gli alunni stessi si pongano ulteriori domande ed è utile che l’insegnante le raccolga, soprattutto se intende approfondire alcune questioni.
come si chiama il poliedro corrispondente al pallone da calcio?
È sorprendente la necessità (a volte quasi impellente) che i ragazzini hanno di dare un nome agli oggetti che imparano a riconoscere. E i nomi di questo poliedro possono far nascere altre domande.
Un nome attribuito a questo poliedro è icosaedro tronco (o troncato): perché?
Una risposta “visuale” (che, a seconda dell’età degli studenti, si potrà tradurre in modo sempre più appropriato nel linguaggio della geometria) si trova nel video qui sotto, tratto dal canale YouTube Mnogogranniki Ru (un canale educativo russo, tutto dedicato ai poliedri). Nel video si mostra come questo poliedro si ottiene a partire da un icosaedro “tagliando via”, intorno a ciascuno dei 12 vertici, una piramide (che sarà a base pentagonale, perché in ogni vertice arrivano 5 facce).
Qualcuno indica questo poliedro come poliedro uniforme (5, 6, 6): perché?
Si tratta di un poliedro uniforme perché intorno a ogni suo vertice arrivano gli stessi poligoni e, inoltre, comunque si fissino due vertici, è possibile rigirare il poliedro in modo da spostare il primo nella posizione del secondo. Queste caratteristiche fanno sì che il poliedro si possa identificare con una serie di numeri che indicano (in ordine) il numero di lati delle facce che arrivano in uno stesso vertice. Il nostro poliedro dunque è un poliedro uniforme di tipo (5,6,6): in ogni vertice arrivano un pentagono regolare e due esagoni regolari.
Quanti sono gli spigoli del poliedro corrispondente al pallone da calcio?
Questa domanda equivale a chiedersi quante sono le cuciture che bisogna fare per costruire il pallone da calcio a partire da pezze esagonali e pentagonali.
Per rispondere, gli alunni possono iniziare a contare spigolo per spigolo, magari aiutandosi con un pennarello per non rischiare di contare lo stesso spigolo due volte. Non è raro, però, che (pensando al pallone da calcio e alle pezze da cucire insieme) in qualche gruppo i ragazzi si accorgano che ogni cucitura unisce due lati, di due pezze diverse. I lati delle pezze esagonali sono 20×6=120; i lati delle pezze pentagonali sono 12×5=60; i lati sono quindi in tutto 180 e le cuciture da fare saranno 180:2=90.
Quanti sono i vertici del poliedro corrispondente al pallone da calcio? C’è qualche legame tra il numero delle facce, degli spigoli e dei vertici?
Contate le facce e contati gli spigoli, si possono contare (uno alla volta, o con qualche strategia che faccia riferimento alla simmetria del poliedro) anche i vertici.
A partire da questo e da altri problemi che abbiano a che fare con il numero di facce, vertici e spigoli di un poliedro, si potranno avvicinare gli alunni alla relazione di Eulero, dando così loro l’occasione di toccare un nodo della matematica profondo e importante, di cui parleremo nella sezione Quasi un libro.
Un problema difficile
La difficoltà di questo problema, inizialmente, potrebbe sembrare di tipo manuale. In realtà i ragazzi si accorgeranno presto che la costruzione di questo solido non è più complicata di quella di tanti altri che si possono fare con cartoncino, forbici e colla: la costruzione di molti solidi, anche se apparentemente più semplici, richiede infatti maggior precisione nei tagli (perché gli angoli delle facce o tra una faccia e l’altra sono più stretti) o nella fase di incollaggio (perché le superfici da incollare sono più sottili o difficili da stringere tra le dita).
La vera difficoltà sta nello scrivere delle istruzioni che servano a qualcuno che non ha potuto vedere il video: occorre osservare bene quanto viene proposto dall’insegnante, provare a ripeterlo (probabilmente più volte) focalizzando l’attenzione sui diversi passaggi che si compiono e trovare un modo per descriverli che sia davvero utile allo scopo. Entrano qui in gioco abilità e competenze linguistiche, perché i ragazzi dovranno fare un uso appropriato ed efficace del linguaggio; ma entrano in gioco anche abilità e competenze che hanno molto a che fare con la matematica e con il pensiero computazionale, per quanto non si vedano numeri, né calcoli, né calcolatori automatici!
Un problema di matematica con effetto sorpresa
Le sorprese suscitate da questo problema possono essere tante, a seconda della classe a cui lo proponiamo.
Chi non ha mai osservato da vicino un classico pallone da calcio e non ha mai notato le cuciture che caratterizzano la sua superficie risulta sorpreso nello scoprire che non si tratta di una sfera perfetta e uniforme, bensì del risultato di tanti singoli poligoni che si inarcano verso l’esterno per effetto della pressione dell’aria interna al pallone stesso.
Molti di quelli che, invece, queste cuciture le hanno già notate si stupiscono del fatto che i singoli pezzi non sono tutti esagoni, anche se con poco sforzo (pensando alla tassellazione del piano in esagoni che si può immaginare guardando i favi di un’arnia o i pavimenti di molte cucine…) si accorgono che, con esagoni soltanto, non si può fare una palla: tre esagoni regolari posti attorno a un unico vertice si uniscono uno all’altro formando una superficie piana.
Quasi tutti si stupiscono, a buon conto, che dal reticolo di soli esagoni si possa costruire il pallone da calcio: non è facile, all’inizio, immaginare che basti lasciare dei buchi pentagonali per ottenere l’effetto desiderato!
Scenari possibili
Questo problema si presta ad essere proposto a livelli molto diversi (meglio se adeguando il tono del racconto e delle richieste all’età dei nostri interlocutori).
Per alunni della scuola primaria, potrebbe essere il coronamento di una serie di attività sui poliedri o sulla geometria solida, mentre per alunni della scuola secondaria potrebbe essere usato come avvio allo studio dei poliedri (per il primo grado) e della relazione di Eulero (per il secondo grado).
Materiale necessario
A fondo pagina è possibile scaricare il file con il reticolo di cui si parla nel video-problema.
È opportuno dare a ogni alunno questo reticolo stampato su cartoncino (quello da 120 g/m2 è dello spessore adatto), in modo da poter costruire il proprio pallone da calcio. È altrettanto opportuno che ogni alunno, o ogni gruppo, riceva qualche copia in più, stampata anche solo su carta, per poterci lavorare al fine di scrivere le istruzioni richieste.
Allegati
Poligoni regolari e frazioni
Antonio, uno studente di seconda media, qualche giorno fa non aveva molta voglia di ascoltare la lezione. Annoiato, stava fissando una pagina vuota del suo quaderno quando all’improvviso, quasi senza rendersene conto, ha esclamato: “Ma guarda! Intorno a ogni punto ci sono esattamente quattro quadrati! Quindi l’angolo del quadrato è 1/4 dell’angolo giro.
Leggi tutto “Poligoni regolari e frazioni”
Allegati
I flaconi di shampoo
Lo shampoo che utilizzate usualmente si trova in due formati e i due corrispondenti flaconi hanno proprio la stessa forma. Avete in casa tre flaconi, uno grande e due piccoli: i due piccoli sono ancora pieni, mentre quello grande è quasi vuoto, c’è proprio solo un fondo. Vorreste travasare i due piccoli in quello grande, ma vi seccherebbe scoprire a metà travaso di doverlo interrompere perché il contenuto dei due flaconi piccoli non ci sta in quello grande.
Leggi tutto “I flaconi di shampoo”
Allegati
Il rombo di carta
Per condividere con gli alunni il video che presenta questo problema, fornire il seguente link:
https://youtu.be/pOAilmWhhEQ
Domande e risposte
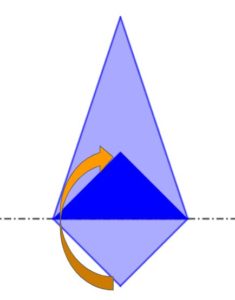
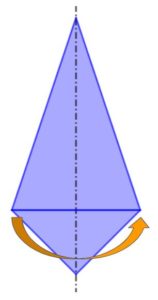
Questo video-problema incomincia con il far osservare ai ragazzi che cosa succede quando si piega un foglio di carta rettangolare con i lati di lunghezze diverse (cioè che non sia un quadrato) lungo una delle sue diagonali e prosegue dando le istruzioni per costruire un rombo.
La professoressa piega a metà il foglio rettangolare (lungo l’asse di due lati), poi piega ulteriormente a metà (con una piega perpendicolare alla prima): ottiene così un rettangolo le cui dimensioni sono la metà di quelle del foglio di partenza.
Piega poi questo rettangolo lungo una delle due diagonali, fingendo di aspettarsi di ottenere un rombo: quando apre il foglio, però, si accorge che le pieghe tracciate disegnano, alla riapertura del foglio, le diagonali e gli assi del rettangolo di partenza, ma… niente rombo!
Ripete (apparentemente) la stessa procedura, ottenendo finalmente un rombo. La domanda che pone, di conseguenza, è questa: “Che cosa è successo? Perché prima non è venuto un rombo? Dove ho sbagliato?”
Il punto è che, riferendosi al rettangolo piccolo ottenuto con le prime due pieghe, non è indifferente piegare lungo l’una o lungo l’altra delle due diagonali. Infatti, se si tiene presente il foglio da cui siamo partiti, la situazione non è più simmetrica:
- una delle due diagonali passa per quel vertice (del rettangolo piccolo) che corrisponde al centro del foglio di partenza; la piega fatta lungo questa diagonale produce le diagonali del foglio rettangolare;
- l’altra diagonale non passa per quel vertice; la piega fatta lungo questa diagonale produce il rombo che ha vertici nei punti medi dei lati del foglio.
Tutte le domande poste successivamente, in realtà, trovano risposta nel video stesso e sono, più che dei problemi da risolvere, degli stimoli a ripensare a quanto visto e sentito, soprattutto se l’insegnante chiederà agli alunni di motivare le proprie risposte. Questi ripensamenti sono volti in particolare a far riconoscere ai ragazzi che la prima impressione visiva che hanno sul quadrilatero ottenuto dalle pieghe, cioè che si tratti di un rombo, è effettivamente corretta: sono proprio le pieghe a garantirci che questo quadrilatero gode delle proprietà che caratterizzano il rombo.
- Come sono i lati del quadrilatero ottenuto? Uguali o diversi? Questo ci basta per dire che si tratta di un rombo?
Il quadrilatero ottenuto con la terza piega ha tutti i 4 lati uguali, perché per l’appunto corrispondono tutti alla stessa piega: proprio per questo motivo siamo sicuri che si tratta di un rombo. - Che angolo formano le diagonali del quadrilatero ottenuto? Lo possiamo stabilire solo grazie al fatto che sappiamo che si tratta di un rombo o anche per come sono state fatte le pieghe?
Le diagonali del quadrilatero ottenuto sono perpendicolari; avendo già stabilito che si tratta di un rombo, non ci sarebbe bisogno di verificarlo, ma si potrebbe anche anticipare questa osservazione e notare che l’angolo tra le diagonali è retto perché esse corrispondono alle prime due pieghe, che sono tra loro perpendicolari. - Come sono gli angoli di questo rombo? Uguali o diversi?
Gli angoli del rombo corrispondono, nel foglio rettangolare di partenza, agli angoli che formano fra di loro le due diagonali. E, se il rettangolo non è un quadrato, questi non sono angoli retti. - Com’è la superficie del rombo così ottenuto in rapporto a quella del foglio rettangolare da cui siamo partiti?
La superficie del rombo è la metà di quella del foglio di partenza; infatti, ciascuno dei quattro rettangoli in cui il foglio di partenza risulta diviso dalle prime due pieghe viene diviso a sua volta dalla terza piega in due triangoli uguali fra loro (la terza piega li sovrappone!) e quindi di uguale area, uno dei quali interno e l’altro esterno rispetto al rombo.
Commenti
Il problema descritto in questo video, per quanto apparentemente sia costruito “solo” attorno alle proprietà del rombo, vuole essere anche una occasione per riflettere sulla simmetria.
La domanda concretamente rivolta agli alunni è solo una, ma vengono proposti molti altri spunti: starà all’insegnante decidere, a seconda della classe che ha di fronte, quanto entrare in profondità sulle diverse questioni che il problema apre.
Un problema significativo
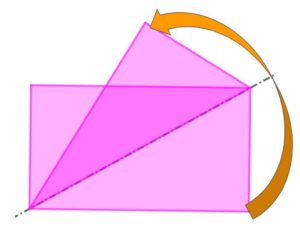
All’inizio del video l’insegnante fa osservare ai ragazzi che, piegando un rettangolo (con i lati consecutivi diversi fra loro) lungo una delle sue diagonali, i vertici opposti che non stanno sulla piega non vanno a sovrapporsi. Non è raro che questo fatto sorprenda i ragazzi: a priori essi sono spesso convinti che, quando si piega il foglio rettangolare lungo la diagonale, le due metà del foglio si sovrappongano.
In effetti, la retta che contiene la diagonale non è un asse di simmetria del rettangolo.
Può sembrare un’osservazione banale, per noi adulti abituati a riconoscere le simmetrie, ma non è detto che lo sia anche per i ragazzini, che spesso invece associano l’idea di asse di simmetria a quella di “retta che divide a metà”, cadendo così in errore, anche sulla diagonale del rettangolo.
Metacognizione
Attraverso le domande che vengono poste agli alunni, non ci si limita qui a fornire delle istruzioni affinché loro, diligenti esecutori, facciano determinate operazioni, ma si stimolano i ragazzi a riflettere su ciò che si sta facendo, a essere consapevoli delle conseguenze di ciascuna azione e del perché si agisce in un modo piuttosto che in un altro.
Questa può essere una buona lezione sull’imparare: non si è imparato qualcosa fino in fondo se non si è capito (oltre al “come” si fa) anche il “perché” si fa in quel modo.
Un percorso a ritroso
Questo problema si può anche considerare un percorso a ritroso, dal momento in cui, volendo motivare le nostre affermazioni, dobbiamo, dopo aver effettuato la costruzione, tornare indietro per comprendere quali sono state le conseguenze delle singole pieghe sulle proprietà delle figure ottenute.
Un problema aperto
ricerca di quadrilateri simmetrici
Il primo fatto che, attraverso il video, l’insegnante pone all’attenzione dei ragazzi è questo: piegando un foglio rettangolare lungo una diagonale, i vertici opposti non finiscono uno sull’altro, non vanno a sovrapporsi. A partire da questa osservazione, come abbiamo visto, possono nascere considerazioni sul tipo di simmetria del rettangolo, ma si può anche ampliare il problema ponendo altre domande, o dando voce alle domande che possono sorgere dai ragazzi.
In particolare, si può chiedere agli alunni: quale forma potrebbe avere un quadrilatero di carta, per essere sicuri che, piegando lungo una diagonale (una qualsiasi? tutt’e due?), i vertici opposti che non stanno sulla piega finiscano col sovrapporsi?
È una domanda che può sembrare banale, ma che – nelle classi in cui l’abbiamo posta – ci ha permesso di tornare su tanti concetti, di dare valore alle immagini che si formano nella mente dei nostri ragazzi quando pensano alla simmetria, ma anche di dare valore alle parole del linguaggio specifico della matematica.
La risposta corretta che più volte abbiamo ricevuto è questa: il foglio potrebbe avere forma quadrata.

Alcuni alunni però si sono spinti anche oltre, proponendo di utilizzare un foglio a forma di rombo.
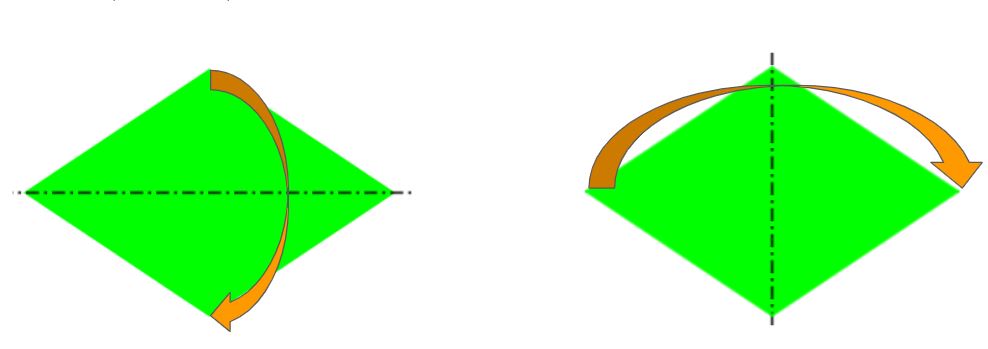
Chi ha avuto la possibilità di coltivare di più la propria immaginazione, riesce a pensare anche a quadrilateri più “strani”. Alcuni alunni, per esempio, hanno pensato a un “quadrilatero formato da due triangoli isosceli attaccati”. Ecco allora che, a partire da risposte come questa, si possono sollecitare interessanti discussioni: è corretta? è sbagliata? va specificato meglio come i due triangoli vanno attaccati? va specificato meglio lungo quale diagonale si piegano?
Come spesso accade, è dalle risposte sbagliate che possono prendere spunto le discussioni più interessanti ed è dalle discussioni attorno alle risposte sbagliate che tutti – insegnanti e alunni – possono acquisire più consapevolezza.
Nelle classi in è stata posta questa domanda, ad esempio, si è andati oltre all’iniziale quadrilatero e alcuni alunni hanno risposto che il foglio poteva avere forma di triangolo isoscele (pensando – giustamente – che il triangolo isoscele ha un asse di simmetria) o poteva essere circolare (pensando – anche in questo caso giustamente – di poter piegare lungo un qualsiasi diametro facendo combaciare esattamente ogni punto di un semicerchio con un punto dell’altro semicerchio). Questa è stata l’occasione per riparlare di diagonali (un concetto tanto semplice quanto facile ad essere frainteso e soggetto a stereotipi), di vertici e di vertici opposti.
considerazioni sulla simmetria del rettangolo
Quando abbiamo chiesto, in classe, di motivare perché, piegando il foglio di carta rettangolare, i vertici opposti che non stanno sulla piega non finiscano col sovrapporsi, non pochi alunni hanno pensato di giustificare il fatto in questione dicendo che “il rettangolo non è un poligono regolare”.
Una risposta di questo genere può essere l’occasione per far riflettere i ragazzi in modo “concreto” sull’implicazione: è vero che il rettangolo non è un poligono regolare e che, quando lo pieghiamo lungo una diagonale, i vertici opposti non vanno a sovrapporsi; è vero anche che il quadrato, invece, è un poligono regolare e che, quando lo pieghiamo lungo una diagonale, i vertici opposti vanno a sovrapporsi; ma… come la mettiamo, per esempio, con il rombo, o con l’aquilone (un quadrilatero con due coppie di lati consecutivi congruenti), che non sono poligoni regolari ma che si possono piegare lungo una diagonale in modo da far combaciare i vertici opposti?
Allenare i ragazzi a questi esempi e controesempi, a distinguere i nessi di causalità dalle semplici concomitanze è una delle occasioni da non perdere che possono essere date da questo problema.
C’è anche un altro motivo per cui ci pare significativo usare la simmetria del rettangolo per giustificare il comportamento del foglio rettangolare quando lo si piega.
Nei percorsi di apprendimento, non sempre viene utilizzata la piegatura della carta per fornire un modello di riflessione: a volte per esempio vengono utilizzati gli specchi, altre volte si fa riferimento solo ai disegni, magari su carta a quadretti. Naturalmente, una volta che il concetto astratto di riflessione si è consolidato, sarà facile passare con agilità da un modello all’altro, ma altrettanto naturalmente non è così quando il concetto si sta formando. Come docenti dobbiamo tenere presente che il confronto fra modelli diversi può essere per i ragazzi una difficoltà non irrilevante e che però è proprio da questo confronto che nasce poi il concetto astratto, sicché è assolutamente importante non stereotipare un concetto su un solo modello, ma cercare di sciogliere, nel tempo, la difficoltà insita nel passaggio da un modello all’altro.
il numero di pieghe e il numero di parti
Nelle classi in cui abbiamo proposto questa attività è stato interessante notare come, dopo aver visto il video, alla richiesta “In quante parti è stato diviso il foglio iniziale dalle 3 pieghe effettuate dall’insegnante?” le risposte non siano state univoche.
Nel video viene ampiamente mostrato il foglio riaperto dopo le tre pieghe: sia nel primo che nel secondo caso esso è diviso in otto triangoli rettangoli uguali fra loro. Eppure, terminato il video, alcuni ragazzi hanno affermato che “il foglio viene diviso in 3 parti, perché sono state fatte 3 pieghe”; e altri hanno ribattuto dicendo che “le parti sono 6, perché ciascuna delle 3 pieghe divide il foglio in due parti e 3 per 2 fa 6”. Cosicché la domanda, posta semplicemente con l’intento di riflettere sul rapporto tra l’area del rombo e quella del rettangolo, ha aperto la discussione in tutt’altra direzione: quella della corrispondenza tra il numero di volte in cui un pezzo di carta viene tagliato a metà e il numero di parti in cui il foglio stesso risulta diviso dalle pieghe.
Le risposte strampalate che abbiamo citato prima possono essere l’occasione anche per un’ulteriore riflessione. Forse i ragazzi di seconda media che hanno risposto in questo modo avevano guardato il video con poca attenzione, probabilmente non avevano provato a riprodurre le pieghe su un foglio, o forse hanno semplicemente attivato quella che a volte ci sembra di poter chiamare la “modalità cervello: off”. È triste, e dal nostro punto di vista paradossale, ma è sotto gli occhi di tutti gli insegnanti il fatto che, a volte, quando i ragazzi sentono una domanda “di matematica”, smettono di ragionare, non pensano più a ciò che hanno visto con i loro occhi o a ciò che potrebbero immaginare a buon senso, e si sentono semplicemente in dovere di usare i numeri che hanno a disposizione per fare un calcolo, non importa quale esso sia.
Del resto, questa strana idea della matematica come qualcosa in cui non serva il ragionamento è molto diffusa, non solo a scuola e non solo tra gli alunni. Quale idea della matematica traspare dalla “Prova di intelligenza” pubblicata su “La Settimana enigmistica” che riportiamo qui sotto?

Uno degli obiettivi che l’insegnante si può porre proponendo problemi su problemi ai propri matematici in erba è proprio quello di sfatare questo falso mito sulla matematica.
Un problema di matematica con effetto sorpresa
Malgrado questo problema probabilmente non stupisca con effetti speciali, una sorpresa c’è ed è proprio all’inizio, nel momento in cui la professoressa sbaglia!
Non che sia sorprendente che una professoressa faccia errori, ma potrebbe esserlo il fatto che lo ammetta, senza spaventarsi, e che – anzi – chieda aiuto agli alunni per comprendere il motivo dei propri errori.
Il fatto che i ragazzi si stupiscano o meno di questo atteggiamento dipende, naturalmente, da come sono abituati: in ogni caso crediamo che sia uno stratagemma che, usato ad arte anche in altre occasioni, può spesso essere utile per richiamare l’attenzione dei ragazzi e quindi anche motivarli a trovare una risposta (magari… “per essere più bravi della prof…”).
Scenari possibili
L’attività di manipolazione proposta in questo video-problema è semplice, per chi ha un minimo di confidenza con la piegatura della carta.
Per bambini della scuola primaria anche il fatto di seguire le istruzioni date per riprodurre le pieghe in modo corretto può non essere banale; per ragazzi della scuola secondaria di primo grado, invece, ad essere sfidanti possono essere le richieste di motivazione.
Materiale necessario
Sarebbe bene che gli alunni guardassero il video avendo a disposizione almeno un paio di fogli di carta rettangolari.
Problemi collegati
Un altro video-problema che ha a che vedere con i rombi e con le piegature della carta è “Una cornice fatta di rombi“, di prossima pubblicazione. Se qui il rombo è il punto di partenza per parlare di simmetria, là diventa l’occasione per parlare di similitudini.
Il salvadanaio magico
Le tre piramidi e il cubo
Per condividere con gli alunni il video che presenta questo problema, fornire il seguente link:
https://youtu.be/-YKYb50LzY8
Soluzione
Ciascuna piramide ha 5 facce: un quadrato, due triangoli rettangoli isosceli uguali tra loro e altri due triangoli rettangoli uguali tra loro.
Ciascuna piramide ha 8 spigoli e 5 vertici.
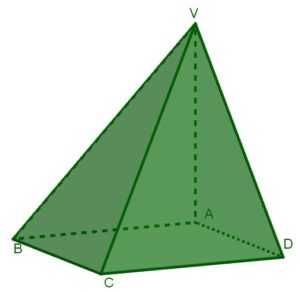
Se lo spigolo del cubo che si ottiene unendo le tre piramidi misura 7 cm, le misure richieste nel problema (facendo riferimento alla figura qui sopra) sono le seguenti:
- i segmenti AB, BC, CD, DA, AV sono tutti spigoli del cubo e quindi misurano 7 cm;
- i segmenti BV e DV sono diagonali delle facce del cubo e misurano 7√2 cm (ossia circa 9,9 cm);
- il segmento CV è la diagonale del cubo e quindi misura 7√3 cm (ossia circa 12,1 cm);
- l’area della base ABCE misura 49 cm2;
- l’area dei triangoli rettangoli isosceli ABV e ADV misura 24,5 cm2;
- l’area dei triangoli rettangoli BCV e DCV misura 24,5√2 cm2;
- il volume della piramide misura 49×7/3 cm3=343/3 cm3 ossia circa 114,3 cm3.
Lo sviluppo piano della piramide descritta può essere rappresentato in modi diversi, ad esempio:
Se indichiamo con s la misura dello spigolo del cubo che si ottiene unendo le tre piramidi, le misure richieste nel problema (facendo riferimento alla figura qui sopra) sono le seguenti:
- i segmenti AB, BC, CD, DA, AV hanno lunghezza s;
- i segmenti BV e DV misurano √2s;
- il segmento CV misura √3s;
- l’area della base ABCE misura s2;
- l’area dei triangoli rettangoli isosceli ABV e ADV misura s2/2;
- l’area dei triangoli rettangoli BCV e DCV misura s2√2/2;
- il volume della piramide misura s3/3.
Commenti
Un problema significativo
“Le tre piramidi e il cubo” permette, manipolando e osservando oggetti molto semplici, di avvicinarsi ad alcuni fatti della geometria solida elementare che tanto elementari non sono.
Per prima cosa, il problema fornisce un esempio concreto di piramide che (pur essendo una semplicissima piramide a base quadrata) è diversa da quelle che fanno parte dell’immaginario collettivo (come le piramidi d’Egitto) e che sono piramidi rette (ossia piramidi nelle quali il piede dell’altezza cade nel centro della circonferenza inscritta nel poligono di base). È buffo vedere come nei libri di testo della scuola media non si lavori mai su piramidi che non siano rette!
In secondo luogo, il problema permette di visualizzare la diagonale del cubo e la diagonale delle facce del cubo. Un altro modello molto utile a questo scopo è quello dello “scheletro” di un cubo costruito, per esempio, con cannucce e scovolini da pipa.
Inoltre questo problema rende visibile, in un caso particolare, il fatto che il volume di una piramide è 1/3 del volume di un parallelepipedo con lo stesso poligono di base e la stessa altezza. Non si tratta di una dimostrazione, chiaramente: è però un buon modo per convincere i ragazzi del fatto che la “formula” che trovano sul libro è plausibile e per rendere quella stessa formula più facile da memorizzare.
Metacognizione
“Le tre piramidi e il cubo” insegna, a proposito dell’apprendimento, che a volte possiamo conoscere meglio qualcosa scomponendolo in parti o, viceversa, componendo parti più semplici a formare un tutt’uno più complesso.
Questa abilità del passare dalla parte al tutto (e viceversa) o da un problema a dei sotto-problemi (e viceversa) si costruisce nel tempo, anche affrontando problemi come questo, in cui la parte e il tutto sono oggetti concreti.
Un problema memorabile
Come si diceva poco sopra, è probabile che i ragazzi, dopo aver toccato con mano le tre piramidi e il cubo che esse formano, ricordino più facilmente il fattore 1/3 nella formula che lega il volume della piramide all’area di base e all’altezza.
Un problema aperto
Una delle direzioni verso le quali è possibile proseguire il discorso aperto da “Le tre piramidi e il cubo” è quella dell’avvio all’algebra.
Nel video viene chiesto ai ragazzi più grandi (immaginiamo quelli della classe terza della scuola secondaria di primo grado, ma tutto dipende dal livello di confidenza raggiunto nell’uso delle lettere come numeri) di esprimere le lunghezze degli spigoli e le aree delle superfici delle facce della piramide in funzione della misura s dello spigolo del cubo.
A meno che i ragazzi abbiano già imparato a memoria eventuali formule presenti sul libro di testo, la cosa più difficile è manipolare l’algebra che permette di determinare, applicando il teorema di Pitagora, le misure della diagonale del quadrato e della diagonale del cubo.
La misura della diagonale BV della faccia del cubo è data da
√(s2+s2)=√(2s2)=√2·√s2=√2·s
La misura della diagonale CV del cubo è data da
√(s2+(√2·s)2)=√(s2+2s2)=√(3s2)=√3·√s2=√3·s.
Se i ragazzi da soli non riuscissero in questa “impresa”, vale la pena di accompagnarli, perché questo calcolo (se non lo si fa diventare un mero esercizio di tecniche imparate a memoria) permette di ritornare sulla definizione di radice quadrata e sul suo significato.
È esperienza comune di noi insegnanti, infatti, quella di ragazzini (e non solo ragazzini!) che sanno calcolare la radice quadrata di quadrati perfetti grandissimi, o sanno approssimare la radice quadrata dei numeri più strani (usando le tavole numeriche, la calcolatrice, o qualche algoritmo imparato più o meno a fatica), ma poi non sanno rispondere a domande come “qual è il quadrato di √3?” o che, per rispondere a domande tipo “qual è la radice quadrata del quadrato di 57?” prima calcolano il prodotto di 57×57 e poi estraggono la radice quadrata.
Trovare l’area delle facce della piramide non dovrebbe creare grosse difficoltà:
- il quadrato di base ha area s2;
- le facce a forma di triangolo rettangolo isoscele sono metà quadrato, quindi hanno area s2/2;
- le altre due facce hanno ciascuna area
(s·√2·s)/2=(√2·s2)/2.
Nelle classi in cui abbiamo proposto questo problema è stato interessante chiedere l’area totale della superficie dello sviluppo piano della piramide. Si è infatti creata l’occasione per rispondere, con un esempio, a una domanda pressante da parte dei ragazzi: a che cosa serve il calcolo letterale? L’espressione che si ottiene applicando la proprietà distributiva alla somma delle singole aree è questa:
(2+√2)s2.
I ragazzi vedono immediatamente che questa espressione, anche se ha richiesto un po’ di “lavoro con le lettere” è più facile da gestire (ad esempio se chiediamo ai ragazzi di disegnarne il grafico o di farlo disegnare ad un foglio di calcolo) rispetto a quella “non semplificata”:
s2+2·(s2/2)+2·(√2·s2)/2.
Inoltre è interessante notare, insieme ai ragazzi, che le due espressioni possono essere entrambe utili per capire cose diverse: se la prima dice immediatamente che la misura della superficie dello sviluppo piano della piramide dipende solo dallo spigolo di base ed è direttamente proporzionale al suo quadrato, la seconda è di lettura meno immediata, ma può essere utile per mettere in evidenza l’area delle singole facce della piramide.
Un problema di matematica con effetto sorpresa
Nel video l’effetto sorpresa è “vanificato” dal fatto che il cubo viene mostrato presto. Ma può essere riconquistato facendo effettivamente costruire ai ragazzi le tre piramidi (una volta scoperto come deve essere lo sviluppo piano) e lasciando che essi chiedano ad amici e parenti se riescono a ricostruire, con esse, un cubo.
Scenari possibili
Il problema è, nel suo complesso, particolarmente adatto alle classi terze della scuola secondaria di primo grado o alle classi prime della scuola secondaria di secondo grado.
Evitando di indugiare sulla domanda che richiede un minimo di confidenza con l’uso delle lettere per esprimere numeri, può essere però anche molto adatto per una classe seconda media, come problema in cui si vede concretamente applicato, in modo significativo, il teorema di Pitagora.
E ancora: se ci si limita alla prima richiesta (contare i vertici e gli spigoli e descrivere la forma delle facce) può essere proposto anche a classi prime della scuola secondaria di primo grado o ad alunni della scuola primaria.
Materiale necessario
Nel caso in cui si chieda ai ragazzi di costruire le piramidi, sono necessari cartoncino, materiale da disegno, forbici e nastro adesivo.
Problema tratto da…
Le tre piramidi e il cubo è tra i Problemi per matematici in erba citati in Diario di bordo (Sofia Sabatti, edizioni mateinitaly, 2020), un testo nel quale alcuni dei problemi presentati in questo sito vengono contestualizzati all’interno di un anno scolastico vissuto da una classe terza della scuola secondaria di primo grado.
La calcolatrice ha sempre ragione?
Paolo deve risolvere questo problema:
27 persone devono andare all’aeroporto in taxi. Ogni taxi può trasportare al massimo 5 persone. Quanti taxi bisognerà chiamare?
Paolo fa il calcolo usando la calcolatrice e poi scrive:
Bisognerà chiamare 5,4 taxi.
Leggi tutto “La calcolatrice ha sempre ragione?”
Allegati
Il patchwork quadrato
La nonna di Alessandra vuole confezionare una coperta quadrata, con la tecnica del patchwork, ossia unendo tramite cuciture tanti riquadri di stoffe diverse. Ha preparato 25 riquadri di stoffe di 5 colori diversi: 5 riquadri per ciascun colore.
Leggi tutto “Il patchwork quadrato”
Allegati
Il fregio di Halloween
Le maestre hanno deciso di decorare la scuola primaria di Tuttinfesta, in occasione della festa di Halloween, con un unico lunghissimo fregio che corre sulle pareti dei corridoi e delle aule.
![]()
Leggi tutto “Il fregio di Halloween”
Allegati
Rombi sul quaderno a quadretti
Quanti sono i diversi rombi con il lato di esattamente 5 quadretti che si possono disegnare sulla carta a quadretti in modo che abbiano tutti i vertici negli incroci della quadrettatura?
Leggi tutto “Rombi sul quaderno a quadretti”
Allegati
Cosa si può fare con cinque quadretti
Luca è arrivato in classe l’altro giorno con questi due disegni, e ci ha raccontato che il suo amico Michel, che abita a Parigi e che è venuto a trovarlo nelle vacanze di Natale, gli ha detto che nella sua classe ne hanno costruiti tantissimi per via di un problema di geometria e che poi li hanno appesi alla parete per decorare la classe.
Leggi tutto “Cosa si può fare con cinque quadretti”
Allegati
Colorare un cubo
Il poliedro in figura (si chiama ottaedro) è colorato a scacchiera: con questo intendiamo dire che è colorato con due colori, in modo tale che due facce che si toccano lungo uno spigolo hanno colori diversi, proprio come in una scacchiera.
Leggi tutto “Colorare un cubo”
Allegati
Sgabelli cubici
A scuola sono arrivati un gran numero di cubi, da usare come sgabelli per una scuola materna; abbiamo a disposizione due colori, il giallo e il blu, e vogliamo colorare i cubi in modo tale che ogni faccia sia tutta dello stesso colore.
In quanti modi diversi li possiamo colorare?
Allegati
Furbetti in coda
Come probabilmente vi sarà già capitato di vedere, a volte all’entrata di un negozio o di un ufficio vengono distribuiti dei numeretti per stabilire in che ordine le persone arrivate saranno servite, in modo da evitare litigi o spiacevoli discussioni.
Leggi tutto “Furbetti in coda”
Allegati
L’ultima cifra
La storia
L’altro giorno Chiara discuteva con due suoi amici; erano presenti anche Alberto, il cugino grande di Chiara, che studia ingegneria all’università, e sua zia, che fa la ricercatrice in matematica. Chiara è ancora alla scuola primaria, ed è una ragazzina sveglia a cui piace giocare con i numeri; prima ha detto ai suoi amici che lei (da vera maghetta) sa che 9x9x9x9x9 è un numero che finisce per 9; e fin qui tutti le han creduto, anche perché lo hanno verificato con la calcolatrice. Ma poi li ha addirittura sfidati in questo modo: Voi ditemi un numero, qualsiasi, anche grandissimo, e io vi so dire qual è l’ultima cifra di 9x9x… moltiplicando tanti 9 quanti ne indica il numero che mi avete detto. E se non è magia questa…!
Leggi tutto “L’ultima cifra”