Sgabelli cubici

Soluzione

Le diverse colorazioni possibili sono 10:

• tutte le facce blu;
• 1 faccia gialla e 5 facce blu;
• 2 facce gialle parallele e le altre 4 facce blu;
• 2 facce gialle adiacenti e le altre 4 facce blu;
• 3 facce gialle aventi un vertice in comune e 3 facce blu aventi un vertice in comune;
• 3 facce gialle disposte “a ponte” (due parallele, opposte tra loro, e la terza adiacente a entrambe) e 3 facce blu ugualmente disposte “a ponte”.
• 2 facce blu parallele e le altre 4 facce gialle;
• 2 facce blu adiacenti e le altre 4 facce gialle;
• 1 faccia blu e 5 facce gialle;
• tutte le facce gialle;

Commenti

È probabile, anche in base a come abbiamo visto affrontare questo problema nelle classi che l’hanno sperimentato, che gli alunni inizino col distinguere i cubi a seconda di quante facce gialle e quante blu vengono usate nel colorarli.
Si ottengono così sette casi:

1. nessuna gialla e 6 blu;
2. 1 gialla e 5 blu;
3. 2 gialle e 4 blu;
4. 3 gialle e 3 blu;
5. 4 gialle e 2 blu;
6. 5 gialle e 1 blu;
7. 6 gialle e nessuna blu.

A questo punto si può osservare che c’è un solo tipo di colorazione possibile per i casi A, B, F, G.

Ci sono invece due colorazioni possibili per ciascuno dei casi C ed E: quando le facce dello stesso colore sono opposte e quando sono adiacenti (questo caso particolare è quello che viene proposto anche nel problema Quattro cubi). Qualche gruppo forse analizzerà i due casi separatamente (non accorgendosi che il caso “4 facce gialle” comporta automaticamente “2 facce blu” e quindi è del tutto analogo al caso “2 facce gialle”), ma è probabile che almeno alcuni gruppi notino la sostanziale equivalenza delle due situazioni e si semplifichino la vita fin dall’inizio.

Resta quindi un solo caso da analizzare, quello con 3 facce gialle e 3 facce blu.
Anche in questo caso ci sono due sole alternative, per quanto possa non essere facile descrivere le due posizioni possibili delle facce dello stesso colore, né argomentare che sono i soli casi possibili:

• le 3 facce blu hanno in comune un vertice (e allora anche le 3 facce gialle hanno in comune un vertice, che sarà il vertice opposto al precedente);
• le 3 facce blu comprendono due facce opposte e parallele; in questo caso non c’è un vertice comune a tutte e tre le facce (e anche le tre facce gialle sono disposte allo stesso modo).

In questo problema, come in tanti altri, è buona cosa che i ragazzi siano lasciati liberi di esplorare le strategie che ritengono più opportune, comprese il ricorrere a disegnare i cubi o i loro sviluppi piani o a costruire e colorare i cubi.

Una obiezione che alcuni gruppi hanno sollevato, durante la sperimentazione, riguarda il considerare il caso in cui tutte le facce sono colorate di giallo e quello in cui tutte le facce sono colorate di blu: poiché il testo parla di due colori, alcuni ragazzi vorrebbero escludere dal conteggio i due casi in cui si usa un solo colore.
Si può naturalmente dire che si tratta solo di mettersi d’accordo sull’interpretazione; tuttavia, analizzando meglio il testo del problema, si può notare che non è scritto che si usano i due colori, ma soltanto che si hanno a disposizione due colori (e quindi si possono usare; il che non vuol dire che si debbano usare).

Un problema significativo

Questo problema, apparentemente molto semplice nella formulazione e nelle richieste, va però a toccare alcuni aspetti fondamentali della matematica che insegniamo nella scuola del primo ciclo:

• la rappresentazione (concreta ma anche mentale) di oggetti tridimensionali;
• il “passaggio” dall’oggetto concreto alla sua rappresentazione bidimensionale;
• il “passaggio” dalla rappresentazione bidimensionale di un oggetto tridimensionale all’immagine mentale e astratta dello stesso;
• il riconoscere figure tra loro uguali;
• il contare quante figure diverse esistano, nel rispetto di determinati vincoli.

Metacognizione

Contando le diverse colorazioni dei cubi, i ragazzi hanno qui l’occasione di imparare qualcosa che vale ogni volta che si devono contare tutti i casi possibili di qualche situazione (un po’ intricata): procedendo in maniera casuale, è facile perdere un caso per strada o contarne un altro due volte e non si ha quindi alcuna garanzia di esaurire tutti i casi che si possono presentare.
“Contare” presuppone quindi il “mettere in ordine” gli oggetti che si devono enumerare (anche se non necessariamente tutte le persone mettono in ordine nello stesso modo); e cercare un ordine è sempre una bella maniera per far sedimentare le nostre idee e appropriarcene meglio.

Strategie risolutive diverse

Le diverse strategie risolutive che abbiamo visto scegliere dai gruppi per affrontare questo problema riguardano il modo di rappresentare i cubi (qualcuno li ha solo immaginati, qualcuno li ha costruiti di cartoncino, qualcuno li ha disegnati) e il modo di contarli, ossia – come si diceva poco sopra – di mettere in ordine le varie possibilità per essere sicuri di prenderle in considerazione tutte, ciascuna una volta sola.

Un problema aperto

Se i ragazzi hanno reagito positivamente al problema, per farli cimentare con qualcosa di analogo si potrebbe far loro studiare il caso del tetraedro: quanti tetraedri diversi si possono colorare, utilizzando solo due colori (e facendo in modo tale che ciascuna faccia sia tutta dello stesso colore)?

Poiché nel tetraedro tutte le facce si toccano, a parità di numero di facce colorate con un dato colore non c’è da distinguere casi diversi: basta contare quante facce sono di un colore e quante dell’altro (e si hanno quindi 5 diverse possibilità).
Nella figura qui sotto si vedono i 5 possibili tetraedri e i loro sviluppi piani, a partire da quello con tutte le facce gialle (a sinistra) fino a quello con tutte le facce blu (a destra).

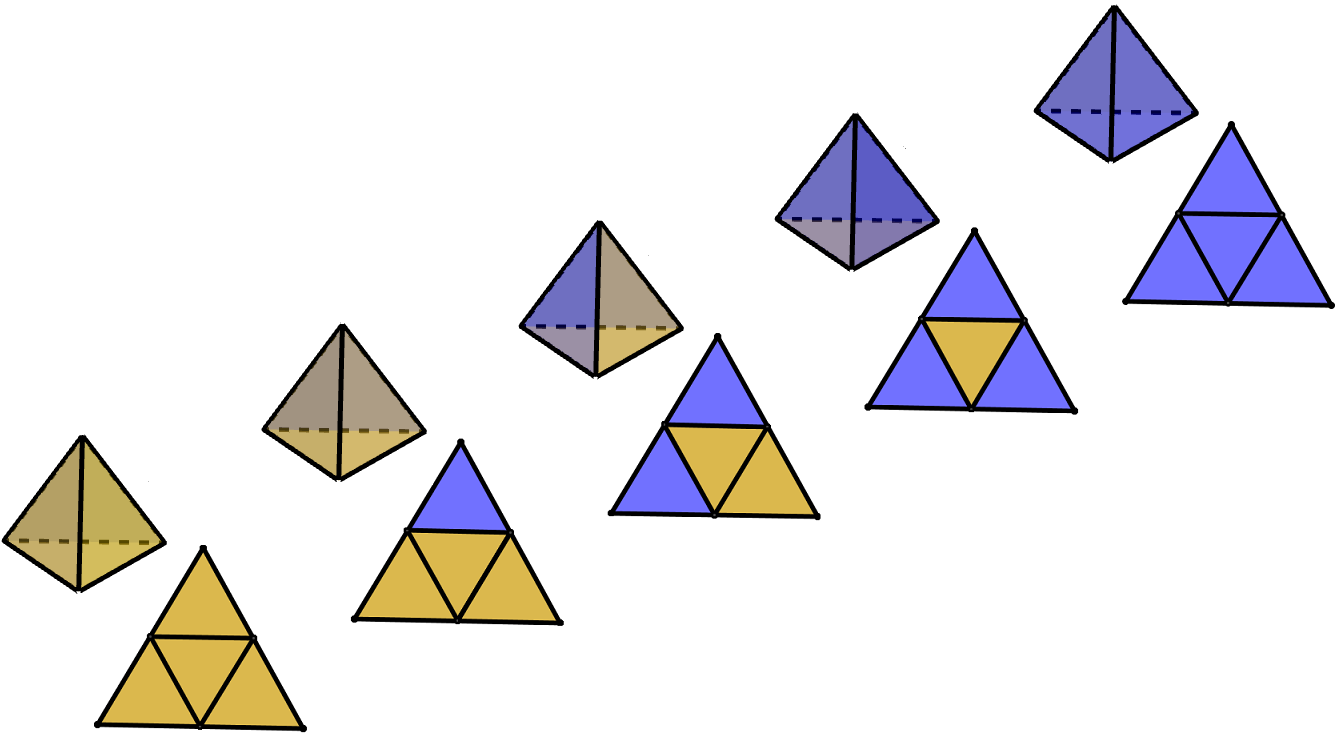
Questa situazione può sembrare più noiosa e meno significativa rispetto a quella che si crea analizzando il cubo; è innegabile però che, per contrasto, metta bene in risalto l’affermazione “nel cubo le reciproche posizioni di due facce sono due: parallele o adiacenti” e che quindi possa essere utile per acquisire consapevolezza sul significato di tale frase.

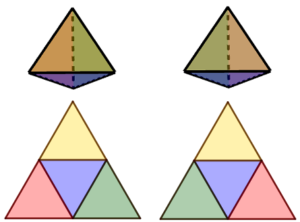
Un altro caso semplice (ma significativo) è quello di un tetraedro, da colorare avendo a disposizione 4 colori. Le possibilità in questo caso sono solo 2 (speculari l’una dell’altra); si tratta di due tetraedri diversi, vista e considerata l’avvertenza iniziale, in base alla quale due oggetti sono colorati alla stessa maniera se possiamo rigirare in mano uno dei due in modo che appaia proprio allo stesso modo dell’altro.

Un problema non standard con effetto sorpresa

Si tratta, secondo noi, di un bel problema perché, pur non essendo difficile da capire e pur non richiedendo strumenti matematici difficili, resta un problema non banale. Abbiamo constatato che spesso i gruppi che l’hanno affrontato erano stupiti di quanti fossero i casi possibili: alcuni erano partiti andando alla rinfusa e, ogni volta che ne saltava fuori uno nuovo, restavano allibiti. L’elenco ben ordinato è molto facile da seguire se qualcuno ce lo racconta, ma il fatto di costruirlo non è immediato per tutti.

E, inoltre, basta un mutamento apparentemente innocuo per farlo diventare un problema assai più complicato (per esempio, se abbiamo a disposizione tre colori invece di due: provare per credere…!).

Sperimentazione e possibili scenari

Questo problema è stato sperimentato in 56 classi terze di docenti partecipanti ai corsi MathUp per la Scuola secondaria di primo grado nell’anno scolastico 2017 / 2018.

“Sgabelli cubici” è stato proposto anche in altre situazioni, sia in contesti scolastici che non scolastici, suscitando interesse e partecipazione anche in ragazzini più giovani. Ad essi può essere proposto con tranquillità, perché il problema, come si diceva, non richiede particolari strumenti matematici e perché il cubo è un solido con cui ben prima di arrivare in terza media i ragazzini hanno una gran familiarità.

Materiale necessario

Cartoncino, colori e forbici possono servire per costruire dei modellini di cubi. Eventualmente si può fornire agli alunni anche delle tessere quadrate di polydron ^[1], perché le usino per costuire dei cubi, ma non è affatto indispensabile.

Se la scuola avesse a disposizione dei dadi in plastica (ad esempio i cubetti bianchi dei regoli) o in legno (ad esempio quelli dei puzzle che possono dare origine a sei disegni diversi), si potrebbero mettere a disposizione degli alunni questi cubi. In tal caso si potrebbero “colorare”, senza rovinarli, appiccicando su ciascuna faccia una etichetta autoadesiva che si possa facilmente togliere.

Problema tratto da…

Questo problema è stato proposto tra i “problemi finali” della sperimentazione legata al corso MathUp per la classe terza della Scuola secondaria di primo grado nell’anno scolastico 2017 / 2018.

Problemi collegati

“Sgabelli cubici” è per molti versi simile al problema Quattro cubi.

Non si tratta di problemi identici: là si passa per lo sviluppo piano dei cubi, al quale invece questo problema non rimanda; qui il numero di facce colorate con un certo colore può variare, mentre in quello ci sono esattamente due facce di un certo colore e le altre quattro di un altro. Identica però è la richiesta (distinguere tutti i tipi possibili di cubi diversamente colorati) e sicuramente simili sono i processi che i ragazzi dovranno mettere in atto per arrivare alla soluzione.

Assegnare prima uno dei due problemi e poi, a distanza di tempo, anche l’altro può essere un’occasione per verificare se e quanto del primo problema sia stato interiorizzato dai ragazzi.

Note

[1] Si tratta di uno strumento, come altri esistenti in commercio, che consiste di tessere poligonali di diverse forme, con la possibilità di incastrarle fra loro.