La calcolatrice ha sempre ragione?

Soluzione

La risposta di Paolo non ha senso, il numero di taxi deve essere un numero naturale. La divisione intera di 27 per 5 ha come quoziente 5 e come resto 2, cioè 27=5⋅5+2, che è come dire che 27 è maggiore di 5⋅5 e minore di 5⋅6. Questo significa che 5 taxi non sono sufficienti e sarà necessario chiamarne almeno 6.

Commenti

Questo problema ha lo scopo di far nascere una discussione tra i ragazzi sulla differenza tra la divisione nell’ambito dei numeri naturali e la divisione nell’ambito dei numeri razionali.

Un problema significativo

Come spesso accade, ci si può accorgere di quanto significativo sia un problema andando a vedere gli errori riscontrati nella soluzione di problemi simili. Per esempio, nella prova di matematica assegnata durante la Rilevazione degli apprendimenti effettuata dall’INVALSI sulle classi quinte dalla scuola primaria nell’anno scolastico 2015 / 2016, è stato assegnato questo quesito:

Soltanto il 35,8% delle risposte registrate erano corrette, e questo può stupirci; ma ciò che indubbiamente ci assicura della necessità di far riflettere i ragazzini sul significato della divisione è il fatto che il 40,5% degli alunni ha ha scelto come risposta la C, in cui il risultato addirittura non è un numero intero.

Metacognizione

Ci sono almeno due “insegnamenti” che i ragazzi possono acquisire affrontando “La calcolatrice ha sempre ragione?” e la cui utilità, però, va ben oltre questo problema.

Il primo di questi “insegnamenti” riguarda il significato degli oggetti matematici e il loro uso in modelli che rappresentano una situazione reale:

• Ogni volta che si ha a che fare con una operazione tra numeri, è bene aver chiaro non solo l’algoritmo che ci permette di eseguire il calcolo, ma ancor più il significato di tale operazione. In questo problema, in particolare, i ragazzi si scontrano con il fatto che l’operazione di “divisione”, pur chiamandosi nello stesso modo quando si opera con i numeri naturali e quando si opera con i numeri razionali, assume due significati diversi. In altri contesti la stessa cosa accadrà con il prodotto, o con la differenza, o con l’estrazione di radice.
• L’operazione di divisione è qui utilizzata per risolvere un problema in un contesto reale e questo pone dei vincoli  sul modello matematico che ha senso usare e sul risultato che possiamo aspettarci. La richiesta del problema riguarda il numero di taxi, cioè di oggetti che si contano e che non possono essere divisi in parti, quindi una risposta sensata deve essere data tramite un numero naturale. Inoltre tutte le persone devono raggiungere l’aeroporto, quindi il quoziente della divisione intera va almeno aumentato di una unità.

Il secondo “insegnamento” riguarda il rapporto con la calcolatrice e, più in generale, con le tecnologie informatiche: ogni volta che si usa una macchina (in questo caso si tratta della calcolatrice, in altri potrebbe essere un computer, un robot …) ci si può anche fidare della sua capacità di eseguire correttamente un compito, ma sta a noi scegliere che cosa farle fare e interpretare il risultato che essa ci restituisce alla luce delle nostre necessità.

Una pluralità di soluzioni

Questo problema non ha un’unica soluzione, perché ogni numero maggiore o uguale a sei e minore o uguale a ventisette (a meno che non si voglia pagare qualche taxi per niente) può essere considerato una risposta corretta.
Questo fatto rende il problema ancor più interessante, perché stimola la discussione tra i ragazzi (all’interno del gruppo di lavoro o nella fase finale di discussione del problema, durante la quale innanzitutto si confrontano le soluzioni ottenute dai diversi gruppi).

Possiamo osservare inoltre che l’insieme delle soluzioni accettabili può essere descritto con precisione tramite disuguaglianze. Usare disuguaglianze non è obbligatorio; in questo problema infatti si potrebbero anche elencare tutte le soluzioni una ad una: sono sufficientemente poche perché si possa ancora farlo. Però elencarle è lungo e noioso, e potrebbe essere naturale per gli studenti iniziare a descriverle attraverso disuguaglianze.  Con questo non intendiamo necessariamente l’uso di simboli quali <, ≤, … Anzi: è forse più significativo e importante che le disuguaglianze vengano espresse a parole, ma in modo sensato e corretto, con espressioni del tipo  “compreso tra… e…”, “almeno…”, “maggiore oppure uguale a…”.

Nella secondaria di secondo grado uno degli argomenti più ostici per i ragazzi è lo studio delle disequazioni, e la difficoltà è dovuta non  tanto all’uso di tecniche complicate, ma soprattutto alla scarsa familiarità con le disuguaglianze numeriche e con il loro significato. La discussione di problemi come questo alla scuola media può contribuire a far acquisire familiarità con l’argomento in modo graduale.

Un problema aperto

Non è un caso il fatto che il testo del problema parli di una calcolatrice: la sottolineatura vorrebbe suscitare simpatia nei confronti del povero Paolo che, pur avendo trovato l’operazione giusta da fare (la divisione) ed essendosi affidato ad uno strumento che, probabilmente, pensava esente da errore, ha finito col dare una risposta grossolanamente sbagliata.
Può essere che, tra gli alunni, sorga una discussione proprio su questo argomento: perché le aspettative di Paolo sono state deluse? La calcolatrice ha sbagliato? Avrebbe potuto Paolo trovare la risposta giusta pur facendo fare i conti alla calcolatrice? Se anche solo un alunno si ponesse queste domande, sarebbe buona cosa non lasciarle cadere nel vuoto.

Innanzitutto si potrebbe chiedere ai ragazzi che legame c’è tra il risultato dato dalla calcolatrice e il numero minimo di taxi che vanno chiamati: questo numero è l’approssimazione all’intero del risultato dato dalla calcolatrice, fatta per eccesso.
Spesso nelle classi, quando si affrontano argomenti come l’approssimazione (per difetto e per eccesso) e l’arrotondamento, gli alunni più spicci vogliono sapere “Ma noi, quale dobbiamo usare?”. Questo potrebbe essere un buon problema per far loro notare come l’arrotondamento non sia sempre la soluzione migliore, pur essendo quella “più vicina” al numero che si sta approssimando, e che non si può fare una scelta “una volta per tutte”, ma bisogna valutare di volta in volta.

Un altro approfondimento interessante che potrebbe nascere sull’uso della calcolatrice è questo: si può usare la calcolatrice per sapere quante persone rimangono a piedi se si chiamano 5 taxi invece che 6? Il che è come chiedere: si può usare la calcolatrice per conoscere, oltre al quoziente, anche il resto di una divisione fatta nell’ambito dei numeri naturali?
La risposta è ovviamente positiva, anche se (quando si ha a che fare con una semplice calcolatrice come quelle che di solito hanno a disposizione i ragazzini alla scuola media) è necessario fare più di una operazione.
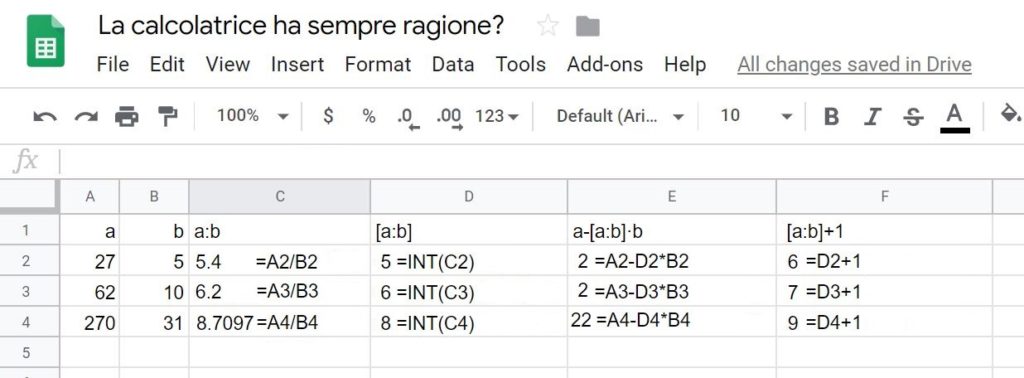
Digitando sulla calcolatrice “a:b=” (dove a e b sono i due numeri naturali in questione) si potrà leggere sul display un certo numero x, risultato dell’operazione fatta dalla calcolatrice. A questo punto sappiamo che il quoziente della divisione a:b pensata nell’ambito dei numeri interi è la parte intera di x, indicata solitamente con [x]. Il resto della medesima divisione è allora dato da a-[x]·b.

Un modo semplicissimo per utilizzare questo problema per un avvio all’algebra e contemporaneamente un avvio al pensiero computazionale è quello di chiedere agli alunni di preparare un foglio elettronico che faccia queste stesse operazioni automaticamente, usando le operazioni di divisione, moltiplicazione, sottrazione e la funzione “parte intera”. Nell’immagine seguente sono evidenziate le istruzioni che possono essere date al foglio elettronico Fogli Google, disponibile gratuitamente on-line.

In alternativa, ovviamente, si possono usare le funzioni “quoziente” e “resto” del foglio di calcolo, che ci permettono di ottenere i risultati richiesti in modo diretto.
Chiaramente, usare il foglio elettronico per fare i conti necessari per rispondere alla domanda del problema è quantomeno fuori luogo: potremmo allora chiedere ai ragazzi di pensare a quali situazioni potrebbero rendere invece davvero comodo far fare i conti ad una macchina.

Scenari possibili

Questo problema riguarda concetti sviluppati nella scuola primaria, ma potrebbe essere molto utile proporlo anche nella scuola secondaria di primo grado, per dare l’occasione ai ragazzi di riflettere sul concetto di divisione nell’ambito dei naturali e sulla differenza rispetto alla divisione nell’ambito dei razionali.

Materiale necessario

Nella sua versione “base”, questo problema non necessita di materiali particolari per essere risolto. Può però essere significativo e interessante che gli alunni abbiano a disposizione (a seconda del contesto in cui si propone il problema) una semplice calcolatrice, un computer con un foglio elettronico o una calcolatrice programmabile, per permettere agli alunni di riflettere su come utilizzare questi strumenti in maniera opportuna.

Problema tratto da…

“La calcolatrice ha sempre ragione?” si ispira a un quesito INVALSI assegnato alle classi quinte dalla scuola primaria nell’anno scolastico 2015 / 2016.
Inoltre è tra i Problemi per matematici in erba citati in Diario di bordo (Sofia Sabatti, edizioni mateinitaly, 2020) un testo nel quale alcuni dei problemi presentati in questo sito vengono contestualizzati all’interno di un anno scolastico vissuto da una classe terza della scuola secondaria di primo grado.

Problemi collegati

La questione toccata da questo problema (la differenza che c’è tra la divisione nell’ambito dei numeri naturali e in quello dei numeri razionali) è ripresa anche nel problema I pasticcini.

Anche i problemi Il fregio di Halloween e L’ultima cifra, cui si rimanda per ulteriori approfondimenti, vertono sulla divisione in N. Per risolvere questi problemi non serve nemmeno considerare il quoziente: l’unico risultato davvero necessario è il resto di alcune divisioni.