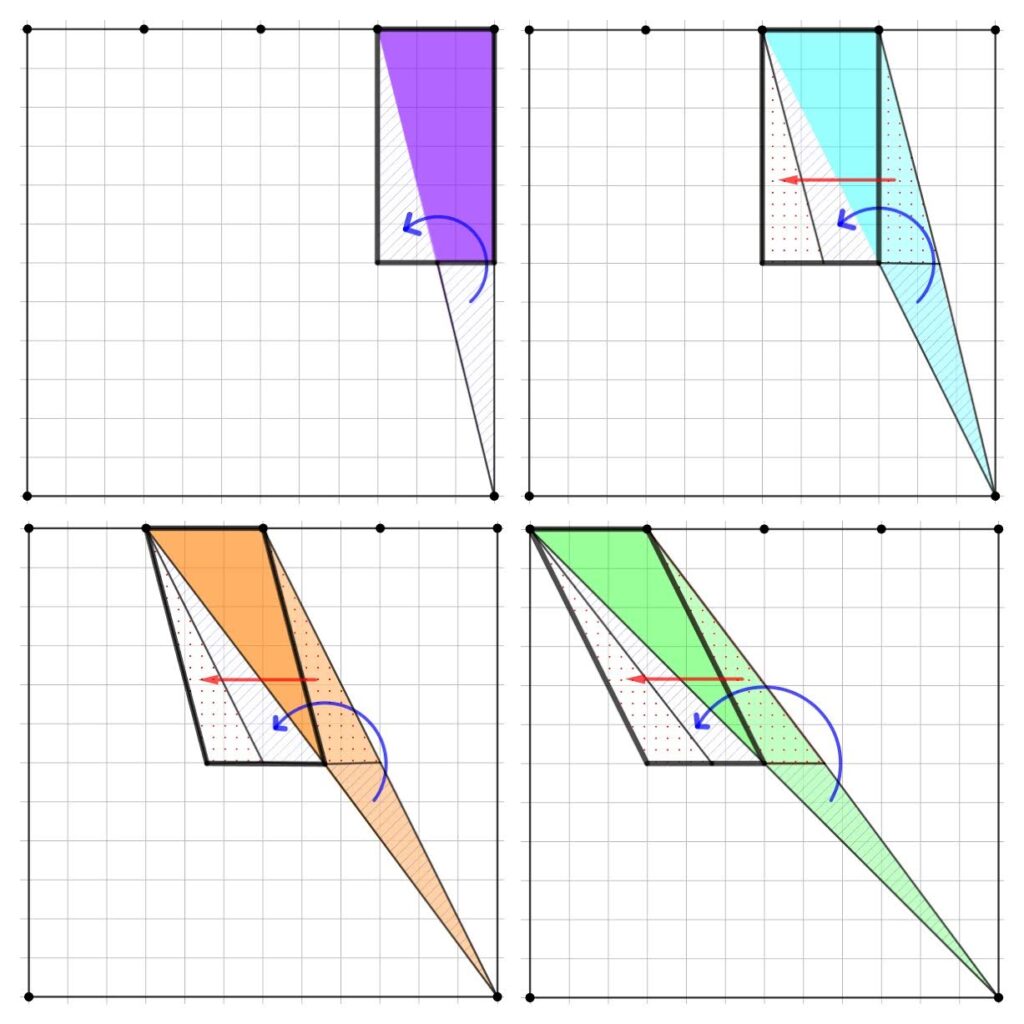
Osservate la figura qui sotto e, in particolare, i quattro triangoli colorati:
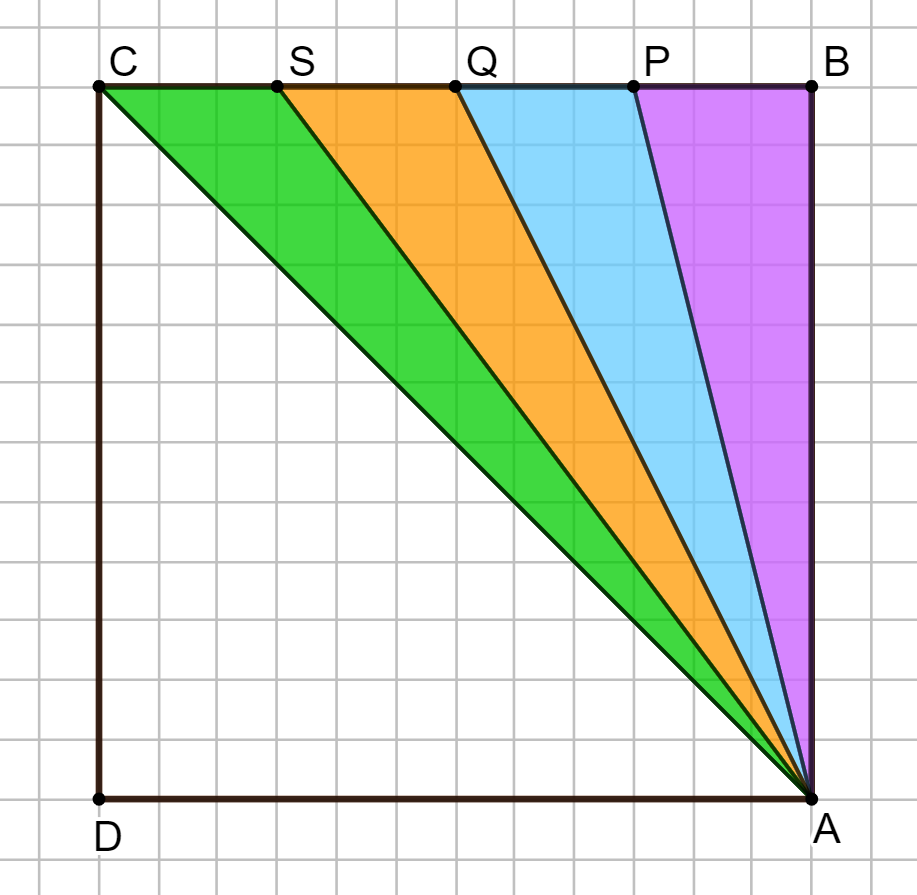
I quattro triangoli hanno uguale perimetro? Se sì, perché? Se no, qual è quello con perimetro maggiore?
I quattro triangoli hanno uguale area? Se sì, perché? Se no, qual è quello con area maggiore?
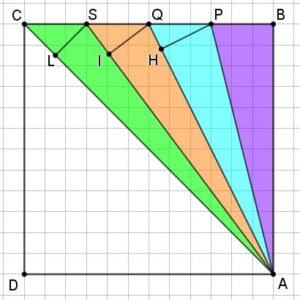
Sapreste indicare, sul lato CD del quadrato, un punto H in modo tale che il triangolo ACH abbia area doppia dell’area del triangolo verde ACS? L’area del triangolo AHD è maggiore, uguale o minore rispetto all’area di ACH?
Fissiamo un’unità di misura in modo tale che l’area del triangolo viola APB valga 1. Quanto vale l’area del triangolo ACH? E quella del triangolo ACD? E quella dell’intero quadrato?
Soluzione
I quattro triangoli ABP, APQ, AQS, ASC non hanno lo stesso perimetro. Il triangolo ASC è quello che ha perimetro maggiore: tutti e quattro i triangoli hanno un lato uguale, cioè BP=PQ=PS=SC, che misura tre lati di quadretto. Inoltre, i triangoli ABP e APQ hanno il lato AP in comune e AQ>AB; i triangoli APQ e AQS hanno il lato AQ in comune e AS>AP; i triangoli AQS e ASC hanno il lato AS in comune e AC>AQ.
I quattro triangoli ABP, APQ, AQS, ASC hanno la stessa area. Per vederlo, scegliamo come base per tutti e quattro i triangoli il segmento contenuto sul lato BC del quadrato: questi quattro segmenti sono uguali fra loro (BP=PQ=PS=SC) e l’altezza ad essi corrispondente nei quattro triangoli è sempre AB.
Il punto H, sul lato CD, che rende l’area del triangolo ACH uguale al doppio dell’area del triangolo ACS è il punto medio di CD.
L’area del triangolo AHD è uguale all’area del triangolo ACH.
Se l’area del triangolo APB vale 1, abbiamo che:
Area (ACH) = 2
Area (ACD) = 4
Area (ABCD) = 8.
Commenti
Un problema significativo
Questo problema fornisce l’occasione di riflettere sui concetti di perimetro e area in un modo che non passa necessariamente per le cosiddette formule. Come approfondiremo nei paragrafi successivi, queste riflessioni scaturiscono, più che dai calcoli, dall’incontro con figure piane non isoperimetriche ma equivalenti e dall’uso di unità di misura non convenzionali.
Non sono pochi gli alunni che, memorizzate alcune procedure, si comportano come se quelle per calcolare l’area e quelle per calcolare il perimetro fossero intercambiabili; l’esperienza ci ha insegnato che mettere i ragazzini di fronte a figure che hanno la stessa area ma non lo stesso perimetro (o, viceversa, hanno lo stesso perimetro ma non la stessa area) fa loro toccare con mano il fatto che queste due grandezze sono diverse e li sprona a stare attenti a non confondere una con l’altra.
Strategie risolutive diverse
Per confrontare i perimetri
Quando si tratta di confrontare i perimetri dei quattro triangoli colorati, alcuni ragazzi ritengono evidente il fatto che il triangolo ASC sia quello con il perimetro maggiore. Ben venga che “vedano” che i quattro triangoli non sono isoperimetrici, ma dobbiamo stimolare questi alunni a fornire anche una spiegazione esauriente della loro intuizione: non possiamo lasciare che si accontentino di motivazioni come “perché si vede”, o “perché ASC ha i lati più lunghi”, o “perché AC è il lato più lungo”, o ancora “perché C è il punto più distante da A”.
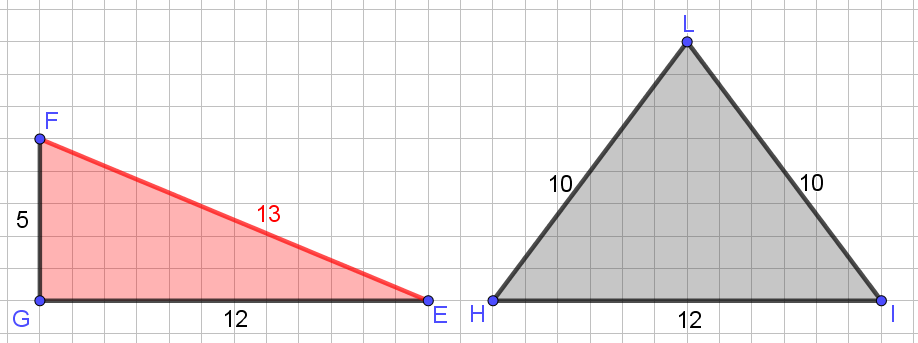
Un buon modo per far capire che certe motivazioni non reggono è quello di fare dei controesempi. A qualcuno che – come è capitato – sostenesse che il perimetro di AQP è maggiore del perimetro di APB perché il lato AQ è più lungo di ciascuno dei lati di APB, si potrebbero mostrare i triangoli EFG e HIL della figura qui sotto: il lato EF è maggiore di ciascuno dei lati del triangolo equilatero HIL, eppure il perimetro di HIL è maggiore del perimetro di EFG (le misure in figura sono espresse rispetto all’unità di misura data dal lato di un quadretto).
Tornando ai triangoli del problema, per dire – per esempio – che il perimetro di APQ è maggiore di quello di ABP non basterebbe dire solo che AQ>AB, ma bisognerebbe notare anche che i due triangoli hanno il lato AP in comune e i lati BP e PQ uguali tra loro. Procedendo così anche per gli altri triangoli coinvolti, si arriva ad affermare che ASC ha il perimetro maggiore di tutti.
Anche se per certi alunni “si vede”, rimane da giustificare perché possiamo dire con certezza che CA>SA>QA>PA>BA. E se questa richiesta, fatta da parte dell’insegnante, può sembrare pedante, facciamo in modo che siano altri alunni a farla! In alcune delle classi in cui è stato proposto questo problema, infatti, non sono mancati ragazzi che hanno davvero (e non per pedanteria) faticato a “vedere” questa catena di disuguaglianze, mentre sembrava loro di “sapere” che in ogni quadrato diagonale e lato hanno la stessa lunghezza; immaginando dunque che CA fosse uguale a BA, deducevano che lo fossero anche i segmenti SA, QA e PA e che i triangoli colorati fossero isoperimetrici. Le strategie utilizzate dai compagni per convincerli sono state diverse:
- ritagliare il quadrato ABCD dal foglio, piegare lungo la bisettrice dell’angolo BÂP per mostrare che PA>BA; successivamente piegare lungo la bisettrice dell’angolo PÂQ per mostrare che QA>PA; e così via;
- puntare il compasso in A con apertura AB per mostrare che PA>BA; successivamente puntare il compasso in A con apertura AP per mostrare che QA>PA; e così via;
- misurare i segmenti CA, SA, QA, PA e BA con il righello, facendo anche notare che “se misuri con il righello la diagonale e il lato di un quadretto del quaderno puoi anche non notare la differenza, ma questo non vuol dire che non ci sia!”;
- utilizzando come unità di misura di lunghezza il lato di un quadretto, calcolare le lunghezze dei segmenti in questione attraverso il teorema di Pitagora.
Se i ragazzi avessero a disposizione un geopiano a quadretti (ovvero una tavoletta ricoperta da piccoli pioli disposti come i vertici di una quadrettatura, attorno ai quali si possono tendere dei cordini), potrebbero mostrare che il cordino necessario per costruire sul geopiano un triangolo ABP non è abbastanza lungo per costruire il triangolo APQ, e così via.
per confrontare le aree
Basi uguali, stessa altezza
Per quanto riguarda l’area, nelle classi in cui il problema è stato sperimentato ci sono stati alunni che hanno notato prontamente che i quattro triangoli ABP, APQ, AQS e ASC hanno la stessa base e la stessa altezza e di conseguenza, visto che l’area del triangolo si trova moltiplicando la base per l’altezza e dividendo il risultato per due, essi hanno anche area uguale.
Il fatto che alcuni compagni ribattessero con affermazioni del tipo “Ma come fanno ad avere la stessa base e la stessa altezza? Non vedete che hanno forme diverse?” ha costretto i primi alunni a precisare meglio: consideriamo BP come base del triangolo rosa, PQ come base del triangolo azzurro, QS come base del triangolo arancio e SC come base del triangolo verde; queste basi sono tutte uguali e l’altezza relativa a queste basi è, per tutti i triangoli, la distanza del vertice A da questi segmenti, che è sempre AB. Per convincere i compagni ancora scettici, alcuni ragazzi hanno rappresentato questa situazione con un disegno che abbiamo riprodotto qui sotto, facendo assumere ai quattro triangoli la stessa forma: hanno fatto scorrere sul lato AD il vertice opposto alla base di ciascun triangolo colorato, mantenendo la stessa base dei triangoli di partenza, e altezza sempre congruente ad AB, dato che AD e BC sono paralleli.
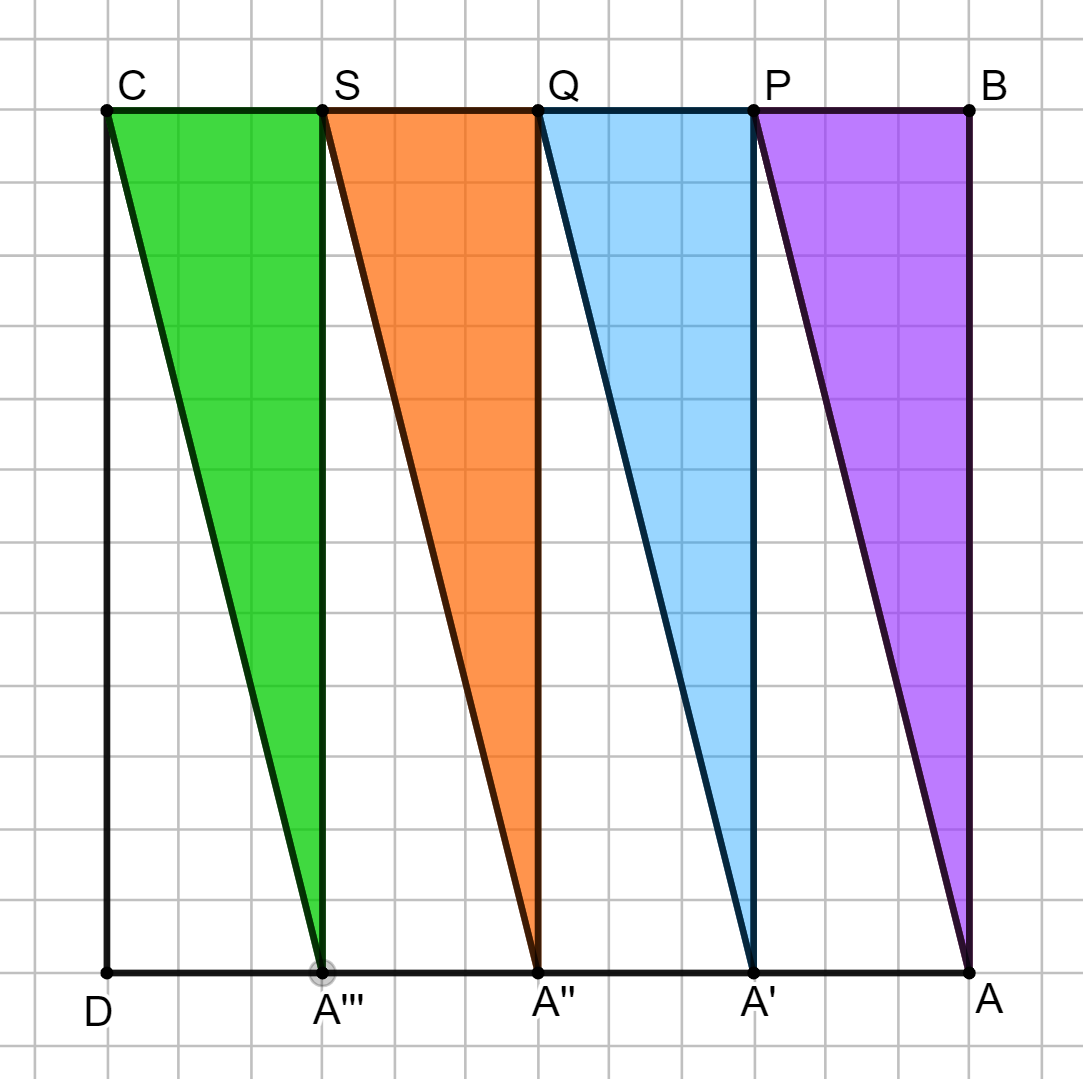
Forse non si tratta di una dimostrazione ortodossa, ma con i compagni scettici è stata efficace!
Triangoli scomposti
Alcuni gruppi di alunni, per dimostrare l’uguaglianza delle aree dei triangoli colorati, non hanno utilizzato l’uguaglianza delle basi (e la formula che conoscono per l’area di un triangolo a partire da base e altezza). Forse perché avevano appena fatto (ed, evidentemente, gradito) un percorso sulla equiscomponibilità, la loro strategia è stata quella di scomporre i triangoli colorati in altri triangoli, ricomponendo i quali hanno costruito quattro parallelogrammi, tutti di base 3 lati di quadretto e altezza 6 lati di quadretto, quindi fra loro equivalenti. La figura qui sotto riproduce i loro disegni, che – in ciascuno dei quattro casi – mostrano in maniera molto esplicita come usare una o più isometrie per ricostruire il parallelogrammo dal triangolo (o viceversa).
I ragazzi avevano già incontrato la formula per il calcolo dell’area del triangolo, e ci immaginiamo che la scelta di procedere per questa via (certamente più complicata rispetto all’applicazione “secca” di una formula) non sia dovuta al fatto di non essere stati capaci di usarla in questa situazione, ma, piuttosto, di avere scelto un metodo che è forse parso a loro più evidente. Qualunque siano state le motivazioni che li hanno portati a questa scelta, il loro lavoro sicuramente evidenzia alcuni aspetti positivi:
- hanno interiorizzato il fatto che due figure equiscomponibili sono equivalenti;
- sono riusciti (seppur in modo informale) a riconoscere triangoli congruenti, sfruttando la quadrettatura del foglio;
- sono anche riusciti (sia pure in modo informale) a utilizzare le isometrie, perché i segni in figura fanno chiaramente pensare, volta a volta, a una traslazione, oppure a una rotazione di 180° che mandi un triangolo nell’altro (giustificando quindi l’uguaglianza dei due triangoli);
- hanno interiorizzato il fatto che parallelogrammi con la stessa base e la stessa altezza sono tra loro equivalenti!
Calcolo dell’area per differenza
Alcuni gruppi di alunni hanno usato come unità di misura i quadretti e, dopo aver calcolato l’area del triangolo viola, hanno calcolato le aree degli altri triangoli colorati come differenze tra aree di triangoli rettangoli, in questo modo:
Area(PBA) = PB·BA:2 = 3·12:2 = 18
Area(QPA) = Area(QBA) – Area(PBA) = QB·BA:2 – PB·BA:2 = 6·12:2 – 3·12:2 = 18
Area(SQA) = Area(SBA) – Area(QBA) = SB·BA:2 – QB·BA:2 = 9·12:2 – 6·12:2 = 18
Area(CSA) = Area(CBA) – Area(SBA) = CB·BA:2 – 3B·BA:2 = 12·12:2 – 9·12:2 = 18
Altre basi, altre altezze
Ad altri alunni è venuto spontaneo considerare come base per i triangoli ottusangoli il lato opposto all’angolo ottuso, ma in questo modo non sono riusciti a calcolare le misure delle aree di tutti i triangoli colorati.
Utilizzando come unità di misura della lunghezza il lato di un quadretto della quadrettatura e come unità di misura dell’area la superficie del medesimo quadretto, gli alunni di un gruppo sono riusciti a ricavare, usando il teorema di Pitagora, le lunghezze dei seguenti segmenti:
AC=√(122+122)=12√(1+1)=12√2
AS=√(122+92)=3√(42+32)=3√25=15
AQ=√(122+62)=6√(4+1)=6√5
AP=√(122+32)=3√(16+1)=3√17
SL=√((3/2)2+(3/2)2)=(3/2)√(1+1)=(3/2)√2
Non sono invece riusciti a calcolare le lunghezze dei segmenti QI e PH, perché i punti I e H non cadono negli incroci della quadrettatura né sono esattamente a metà quadretto (come accade invece al punto L). Quindi hanno calcolato l’area di soltanto due dei triangoli colorati:
Area(ABP)=AB·BP:2=12·3:2=18
e
Area(ASC)=AC·SL:2=12√2·(3/√2):2=12·3:2=18.
Un altro gruppo di alunni che ha voluto utilizzare le stesse basi e le stesse altezze ha proceduto misurando queste basi e queste altezze con il righello e calcolando poi le aree dei triangoli colorati di conseguenza. Così facendo questi ragazzi hanno ottenuto valori “vicini” ma diversi e non hanno pensato che questo fosse dovuto alla necessaria imprecisione delle misure effettuate, ma al fatto che – come i perimetri – anche le aree fossero diverse.
La strada seguita da questi gruppi, in entrambi i casi, si è rivelata poco efficace per la soluzione del problema, ma ricca di spunti di riflessione. Proviamo a riassumere qui di seguito alcuni di quelli che sono emersi durante la discussione con il resto della classe e il confronto delle diverse strategie risolutive.
- I ragazzi che hanno usato come basi i segmenti CA, SA e QA hanno ammesso di non averlo fatto per scelta, ma perché proprio non erano riusciti a vedere altre possibili basi. Crediamo che questa rigidità possa dipendere – almeno in parte – dalla poca varietà degli esempi (nel caso specifico di triangoli ottusangoli) che gli alunni hanno incontrato nei precedenti anni di scuola e da una scarsa confidenza con il concetto di altezza. Ben venga questo problema e ben vengano problemi analoghi, dunque, in cui i triangoli ottusangoli non siano disegnati con il lato maggiore parallelo ai bordi inferiore e superiore del foglio e in cui l’altezza più comoda da considerare non sia quella interna al triangolo!
- Solo pochi ragazzi, tra quelli dei gruppi che hanno fatto questa “scelta”, sono riusciti ad applicare correttamente il teorema di Pitagora e a gestire tutti i calcoli con i radicali riportati sopra. Sicuramente questa strada era più lunga, implicava maggior fatica e forniva più occasioni in cui un semplice errore di calcolo poteva portare a un risultato sbagliato. Confrontandosi con i compagni, anche quei pochi che sono riusciti a fare i calcoli hanno dovuto ammettere che, prima di imbarcarsi a far conti su conti, conviene pensare per bene e vedere se non ci sono altre possibilità. Del resto, una delle citazioni erudite che affascina di più i ragazzini è proprio quella secondo la quale “La matematica è l’arte di non fare i calcoli“, attribuita a Oscar Chisini.
- I ragazzini del gruppo che era riuscito a calcolare solo le aree dei triangoli verde e viola hanno difeso la propria strategia dicendo, più o meno, così: “Non siamo riusciti a calcolare l’area dei due triangoli che stanno in mezzo, ma vedendo che quella del primo e dell’ultimo sono uguali, saremmo pronti a scommettere che lo siano anche quelle dei due triangoli nel mezzo.” Da qui è nata una bella discussione, in classe, a proposito della differenza che c’è tra l’essere certi di qualcosa e l’intuirlo soltanto, magari al punto di essere pronti a scommetterci.
- È stato difficile far accettare agli alunni che misurare con il righello i lati dei triangoli potesse andare bene per dimostrare che i loro perimetri fossero diversi, ma misurare con il righello le loro basi e le loro altezze non andasse altrettanto bene per dimostrare che le loro aree fossero uguali. Effettivamente la situazione è delicata ed è buona cosa che – attraverso questo o altri problemi – emerga. Le misure che si ottengono in maniera diretta, confrontando con il righello il disegno di un segmento, sono necessariamente approssimate; se due misure effettuate in questo modo sono molto diverse, potremo ragionevolmente essere certi che siano diverse anche le grandezze che abbiamo misurato, ma se sono poco diverse non potremo arrivare alla stessa conclusione. La difficoltà in tutto questo sta nel fatto che il significato di “molto” e di “poco” non è assoluto ma dipende dalla sensibilità e dall’errore strumentale del nostro righello.
- Questo problema si è rivelato utile per confermare quanto abbiamo riscontrato anche in altre situazioni, ossia il fatto che alcuni alunni ancora non riempiono di significato la parola “area” e la parola “uguale”. Per alcuni alunni, infatti, sembra non costituire una contraddizione il fatto che le aree dei triangoli colorati siano tutte uguali se si usano, per calcolarle, certe basi e certe altezze e siano invece diverse se si usano, per calcolarle, altre basi e altre altezze. L’impressione che se ne ha è che per questi alunni l’area sia semplicemente il risultato di una operazione: non stupisce, quindi, che da operazioni tra termini diversi si ottengano risultati diversi. Questo indica, però, che almeno per questi ragazzi c’è bisogno ancora di altri esempi e ancora di altri problemi che, come questo, facciano davvero toccare con mano che cosa significa area (e non solo come si calcola l’area) e che cosa significa uguaglianza.
Un percorso a ritroso
L’ultima parte del problema propone due richieste di quelle che chiamiamo “a ritroso”: invece di assegnare i vertici di un poligono e chiedere di calcolarne l’area, si fa il viceversa; e invece di scegliere l’area di un quadrato come unità di misura, si sceglie l’area di un triangolo e si chiede di calcolare di conseguenza quella di un quadrato.
Queste richieste possono risultare spiazzanti e in questo sta la loro utilità: sono domande che attirano l’attenzione dei ragazzi, stimolano il loro pensiero, li costringono a fare delle scelte; e nell’essere protagonisti delle scelte che fanno, riflettono di più e imparano di più.
alla ricerca di un punto
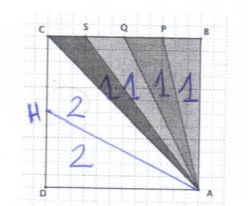
Dopo tutte queste riflessioni sull’area dei quattro triangoli colorati, i ragazzi individuano facilmente il punto H, sul lato CD, che fa sì che il triangolo ACH abbia area doppia dell’area del triangolo verde ACS. Se la precedente discussione è stata proficua, dovrebbero essersi accorti che il punto H si individua facilmente perché, se consideriamo CH come base del triangolo ACH, esso ha la base CH doppia rispetto alla base CS del triangolo ACS, e l’altezza AD uguale ad AB, perché ABCD è un quadrato.
L’area del triangolo AHD è uguale all’area del triangolo ACH perché essi hanno la base uguale (DH=HC) e la stessa altezza AD, situazione analoga a quella precedentemente discussa relativamente ai quattro triangoli colorati.
una strana unità di misura
L’ultima parte del problema attira l’attenzione dei ragazzi sul concetto di unità di misura e sul significato dell’azione misurare. È probabile (anche se non certo, perché il problema non lo richiede) che, durante lo svolgimento del problema, sia stato detto che l’area di ciascuno dei triangoli colorati è 18 quadretti. Ora dobbiamo porre quest’area uguale a 1, cioè farla diventare la nostra unità di misura, e confrontare con essa le aree delle altre figure in gioco, esprimerle in funzione della nostra unità di misura.
Quante volte i ragazzi avranno letto sui loro libri che misurare significa confrontare una grandezza con un’altra, a essa omogenea, presa come unità di misura! Ma avranno capito il significato di queste parole? Istintivamente, potrebbero aver considerato il quadretto come unità di misura, durante lo svolgimento del problema. Cosa succede se cambiamo l’unità di misura? Cambieranno semplicemente i numeri che esprimeranno il rapporto, il confronto, tra la grandezza che stiamo considerando e l’unità di misura. Per esempio, se la nostra unità di misura è il quadretto, l’area di APQ assumerà il valore di 18, mentre se la nostra unità di misura è l’area di ABP, l’area di APQ assumerà il valore di 1. Non cambieranno però i rapporti tra le aree delle varie figure in gioco, espresse in funzione della stessa unità di misura.
Quindi, se l’area del triangolo APB vale 1, abbiamo che:
Area (APB) = Area (APQ) = Area (AQS) = Area (ASC) = 1
Area (ACH) = 2Area (ASC) = 2 = Area (AHD)
Area (ACD) = 2Area (ACH) = 4
Area (ABCD) = 2Area (ACD) = 8
Metacognizione
Quando parliamo di misure in quadretti, solitamente diamo per scontato che ci stiamo riferendo al lato del quadretto o all’area del quadretto in base al contesto del problema in cui stiamo lavorando e diciamo indifferentemente che “un’area misura 18 quadretti” e che “un lato misura 3 quadretti”.
Questo problema, in cui si parla sia di area che di perimetro, potrebbe essere l’occasione per sentire la necessità di specificare meglio e di riferirsi, quindi, all’unità di misura delle aree come quadretto, a quella delle lunghezze come lato di quadretto.
In alcune delle classi che hanno sperimentato questo problema, l’esigenza di evitare fraintendimenti è stata sentita ed esplicitata proprio da alcuni ragazzi: come non accontentarli? Viceversa, se tutti gli alunni fossero già abituati a usare la stessa parola per indicare l’unità delle due diverse misure, senza rischio di ambiguità, probabilmente non varrebbe la pena appesantire il discorso con questa distinzione. Del resto il termine ounce (oncia) indica due diverse unità di misura ancora d’uso comune negli Stati Uniti d’America, una per il peso e una per il volume.
Un problema aperto
Possiamo stimolare una riflessione ulteriore chiedendo ai ragazzi: mantenendo sempre l’unità di misura che abbiamo considerato nell’ultima parte del problema, cioè quella per cui l’area di ABP vale 1, come possiamo trovare il segmento di lunghezza 1, ovvero il lato di un quadrato di area 1? Ragionando su questo quesito, i ragazzi possono consolidare l’idea che questi due “1” hanno un significato ben diverso: il primo si riferisce a una misura di area, il secondo a una misura lineare, di lunghezza. E potranno anche visualizzare questo concetto.
Gli alunni a cui è stato proposto questo quesito, hanno cercato il quadrato di area 1, per poi considerare il suo lato, di lunghezza 1.
Le immagini seguenti riproducono due soluzioni grafiche fornite da due gruppi di alunni:
La fotografia qui sotto, invece, rappresenta la soluzione fornita da un gruppo di alunni piegando la carta; con il metodo della piegatura, si evidenzia anche che il quadrato ABCD è formato a sua volta da 8 quadrati di area 1: cinque interi, due divisi a metà (lungo i lati del quadrato ABCD), uno diviso in quattro parti (ai vertici del quadrato ABCD).
Problema tratto da…
Il problema trae ispirazione da un quesito della prova INVALSI somministrata agli alunni delle classi terze della scuola secondaria di primo grado nel 2014:
A volte, la difficoltà a riconoscere che in ogni triangolo uno qualunque dei tre lati può essere considerato come base (e che quindi ci sono tre altezze, una in corrispondenza di ciascuna base), non viene superata nemmeno durante la scuola secondaria di primo grado. A dimostrazione del fatto che non si tratta di una eventualità così rara ci sono i risultati di un quesito assegnato nella prova INVALSI del 2012 agli studenti del secondo anno della scuola secondaria di secondo grado:
Solo il 28,1 % degli alunni cui è stato sottoposto questo quesito ha risposto correttamente, ossia ha riconosciuto che tutti gli infiniti triangoli di base AB con il terzo vertice sulla retta parallela ad AB e passante per C hanno la stessa area di ABC.
Ben il 53,3 % degli alunni, invece, ha risposto che soltanto il triangolo ABC’, simmetrico di ABC rispetto all’asse di AB, ha la stessa area di ABC, evidenziando così sia l’errore concettuale di chi immagina che due triangoli aventi un lato in comune sono equivalenti solo se sono congruenti, sia una mancata interiorizzazione del concetto di altezza.
Sperimentazione e possibili scenari
Il problema Quanto sono grandi questi triangoli? è stato sperimentato nell’anno scolastico 2021 / 2022 da alcune classi seconde della scuola secondaria di primo grado, nell’ambito del corso MathUp “Problemi di Matematica: un gioco da ragazzi”, come esempio di problema che richiede di applicare il processo Misurare.
Non richiedendo particolari pre-requisiti potrebbe essere proposto anche in una classe quinta della scuola primaria, onde evitare che si formino quelle rigidità di cui si diceva tra i commenti, per le quali l’unico lato che i ragazzini riescono a considerare come base di un triangolo ottusangolo è quello più lungo.
E così pure potrebbe essere proposto anche al biennio della scuola secondaria di secondo grado, qualora fosse necessario sciogliere eventuali rigidità già formatesi e convincere i ragazzi che è necessario saper riconoscere tutte le altezze dei triangoli per poter, di volta in volta, scegliere quella che è più comodo considerare, in funzione del particolare problema che si sta affrontando.





Problema interessante per i miei ragazzi di seconda, settimana lo proporrò sicuramente in classe.
Grazie!
Benissimo, Chiara! Ci faccia sapere come va, se può! In particolare saremmo curiose di sapere se i suoi alunni trovano altre strategie, o hanno qualche difficoltà particolare, o fanno qualche errore che le sembra opportuno valorizzare!
L’ha proposto anche io in una terza però, giusto per vedere cosa ricordavano. Problema molto interessante e i ragazzi .
Non tutti i ragazzi han capito che l’altezza fosse comune, ma è stato bello vedere come discutevano tra loro per confrontare le diverse opinioni.
Sono contenta che sia stato bello, anzi: credo che uno dei motivi per cui il nostro mestiere è bello sia proprio il fatto che ci dà la possibilità di vedere i ragazzi discutere, confrontarsi. E i problemi come questo sono un’ottima occasione per fare in modo che queste discussioni avvengano sempre di più sul piano dell’argomentazione e per verificare – oltre a che cosa i ragazzi ricordano di quanto appreso – quanto abbiano fatto proprio l’atteggiamento del matematico, che cerca di scoprire e dimostrare.