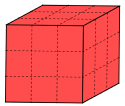
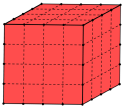
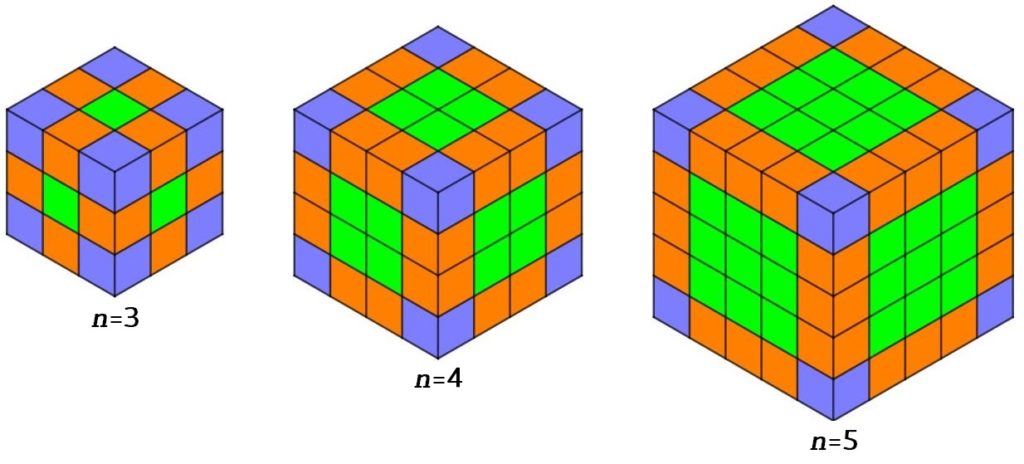
Partiamo da un cubo, coloriamone la superficie esterna di rosso e affettiamolo in cubetti, dividendo ogni spigolo in tre parti uguali, come in figura.
Siete d’accordo che i cubetti in totale sono 27 e che, fra questi, ce n’è uno solo (al centro) che non ha facce rosse, ce ne sono 6 con una sola faccia rossa, 12 con due facce rosse, 8 con tre facce rosse, e nessuno con più di tre facce rosse?
Immaginate ora di affettare il cubo in cubetti partendo da una divisione di ogni spigolo in 4 parti uguali, come in quest’altra figura: quanti cubetti si ottengono in tutto? Quanti di questi non hanno alcuna faccia rossa? Quanti ne hanno una sola? Quanti ne hanno due? Quanti ne hanno tre? Quanti ne hanno più di tre?
E come si continua? Fissiamo un numero n (n è un numero naturale, maggiore di 2, non sappiamo quale), cominciamo a dividere ogni spigolo in n parti uguali, e poi affettiamo il cubo in cubetti partendo da questa suddivisione (come si è fatto nelle due figure per i casi n=3 e n=4). Come potreste indicare il numero totale dei cubetti? E il numero di quelli che non hanno alcuna faccia rossa? che ne hanno una sola? che ne hanno due? che ne hanno tre? che ne hanno più di tre?
Soluzione
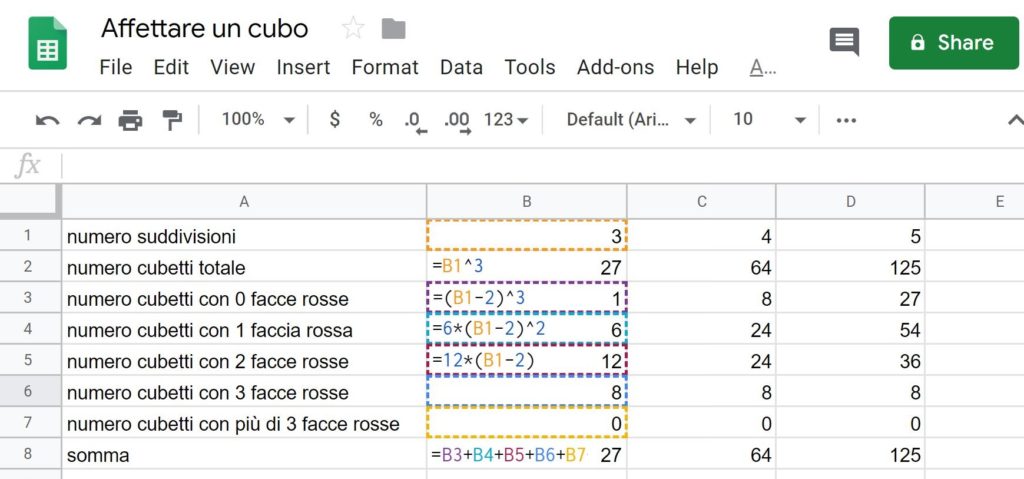
| Numero di parti in cui è diviso lo spigolo | 4 | n |
|---|---|---|
| Numero di cubetti | 64 | n3 |
| Numero di cubetti senza facce rosse | 8 | (n-2)3 |
| Numero di cubetti con una faccia rossa | 24 | 6(n-2)2 |
| Numero di cubetti con due facce rosse | 24 | 12(n-2) |
| Numero di cubetti con tre facce rosse | 8 | 8 |
| Numero di cubetti con più di tre facce rosse | 0 | 0 |
Commenti
Un problema significativo
“Affettare un cubo” è un problema particolarmente bello perché tocca e mette in relazione due nodi significativi dell’apprendimento della matematica: quello legato alla visualizzazione spaziale (al sapersi immaginare figure tridimensionali e la loro struttura) e quello legato all’algebra, in particolare all’uso delle lettere per esprimere relazioni tra numeri.
La conoscenza della struttura del cubo (ossia del fatto che ha 8 vertici, 6 facce e 12 spigoli) ha un ruolo cruciale nella soluzione; la maniera in cui nel testo si illustra il caso n=3 ha proprio lo scopo di far emergere questa struttura, suggerendola soltanto, senza richiamarla esplicitamente.
L’uso delle lettere come variabili è l’altro tema forte che è possibile far incontrare ai ragazzi attraverso questo problema: il linguaggio algebrico permette di esprimere in modo sintetico e chiaro le relazioni che si possono trovare grazie alla conoscenza della struttura del cubo.
Strategie risolutive diverse
Prima di rispondere, i ragazzi potrebbero aiutarsi analizzando qualche figura, o qualche modello.
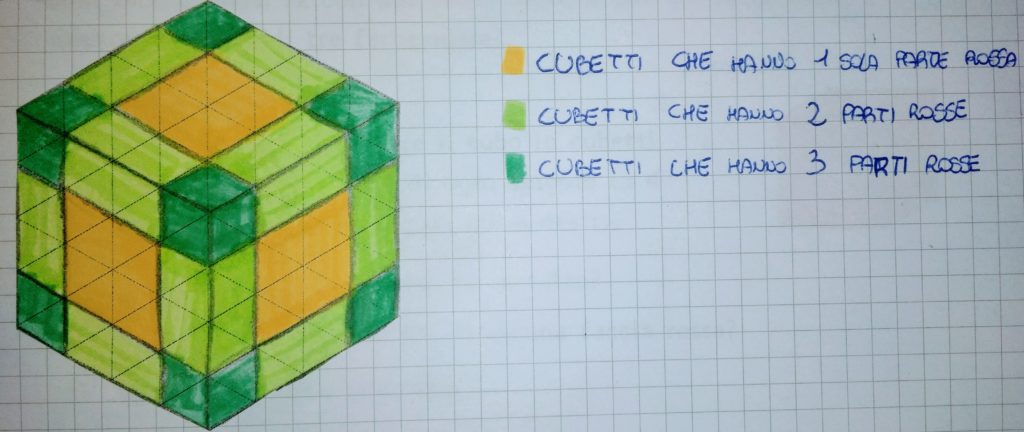
La figura qui sotto riportata, ad esempio, è stata disegnata su carta isometrica da un gruppo di ragazzi di terza media che hanno affrontato questo problema. Le facce visibili dei cubetti con una sola faccia colorata sono state evidenziate in giallo, quelle dei cubetti con due facce colorate sono state evidenziate in verde chiaro e quelle dei cubetti con tre facce colorate sono state evidenziate in verde scuro.
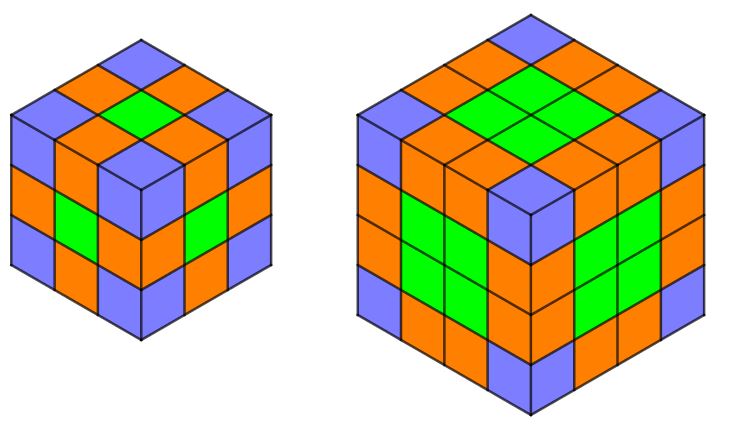
Un altro gruppo di ragazzi ha avuto un’idea simile (colorare con colori diversi le facce visibili di cubetti con un diverso numero di facce colorate), ma ha realizzato il disegno con GeoGebra, sia per il cubo con gli spigoli divisi in 3 parti uguali che per quello con gli spigoli divisi in 4 parti uguali.
Dall’analisi di queste o altre figure, o con l’aiuto di qualche modello, o anche solo basandosi sulla propria immaginazione, gli alunni si possono convincere del fatto che:
- in totale i cubetti sono n3;
- non ci sono cubetti con più di 3 facce rosse (quando n>1);
- i cubetti con 3 facce rosse sono 8, uno per ciascun vertice del cubo, e sono sempre 8, qualunque sia il valore di n (con n>1);
- i cubetti con due facce rosse sono in corrispondenza degli spigoli: gli spigoli sono 12 e (quando n>2) su ciascuno ci sono n-2 cubetti con due facce rosse, perché occorre togliere i due in corrispondenza dei vertici del cubo;
- i cubetti con una sola faccia rossa sono in corrispondenza delle 6 facce e il loro numero per ogni faccia è (n-2)2 , perché occorre togliere dal quadrato la “cornice” esterna, composta da cubetti che hanno 2 oppure 3 facce colorate di rosso;
- i cubetti in cui nessuna faccia è colorata di rosso formano (all’interno del cubo dato) un altro cubo, affettato in cubetti, proprio come quello da cui siamo partiti, ma un po’ più piccolo; lo si può ottenere partendo da una divisione del suo spigolo in n-2 parti uguali invece che in n: è composto quindi da (n-2)3 cubetti.
Naturalmente questa non è la sola via in cui si può procedere. I ragazzi potrebbero raccogliere un po’ di dati, cominciando a esaminare cosa succede per valori piccoli di n, osservare le regolarità numeriche che compariranno e ipotizzarne un proseguimento. In questo problema però (rispetto a quanto accade in Affettare un quadrato) il conteggio esplicito, anche già per n = 5 o per n = 6, può essere più complicato, e comporta numeri più grandi; e, in ogni caso, servirà poi una conferma per avere la certezza che l’ipotesi circa il come proseguire sia un’ipotesi fondata.
Metacognizione
Molto spesso accade che, più i numeri di un problema sono piccoli, più noi e i nostri ragazzi consideriamo quel problema “facile”. E non abbiamo tutti i torti!
“Affettare un cubo”, però, è un buon esempio di come a volte sia bene mettere in discussione questa certezza granitica: in questo caso, infatti, è proprio andando a vedere che cosa accade quando i numeri sono più grandi che diventa più evidente il nesso fra le richieste del problema e la struttura del cubo. Lo si vede bene dall’immagine seguente, che “completa” – aggiungendo il caso n=5 – quella costruita con Geogebra da un gruppo di ragazzi di terza media.
Ecco, dal punto di vista dell’imparare a imparare, può essere una bella conquista accorgersi che non sempre più i numeri di un problema sono grandi, più il problema diventa difficile da risolvere: qualche volta, i numeri grandi possono essere nostri alleati nella comprensione profonda di un problema!
Una pluralità di soluzioni
Anche se le risposte alle domande di questo problema sono sostanzialmente univoche, gli alunni potrebbero esprimerle in modi diversi.
Nelle classi che abbiamo direttamente seguito quando hanno affrontato questo problema, è stato frequente, per esempio, il calcolare il numero di cubetti senza alcuna faccia rossa “per differenza”, ossia togliendo dal numero totale dei cubetti il numero di quelli con 1, 2 o 3 facce rosse:
n3-[6(n-2)2+12(n-2)+8]
oppure
n3-6(n-2)2-12(n-2)-8.
Interessante, nell’ottica di un avvio al calcolo letterale, può essere il confrontare le diverse espressioni ottenute per capire se sono uguali tra loro oppure no.
Un problema aperto
Nelle classi alle quali abbiamo proposto questo problema, gli alunni stessi si sono posti ulteriori domande, a volte per curiosità, altre volte solo per essere sicuri di aver dato la risposta giusta alle richieste del testo. Vediamo di seguito alcune di queste questioni.
Verso la verifica
Quando “Affettare un cubo” è stato proposto a classi che non avevano ancora piena confidenza con il linguaggio algebrico, alcuni gruppi di ragazzini non si sentivano sufficientemente sicuri nel tradurre in una espressione letterale pensieri come “le facce rosse dei cubetti con una sola faccia rossa formano, su ciascuna faccia del cubo originale, un quadrato; questo quadrato ha il lato più corto di quello della faccia del cubo originale; precisamente, è più corto di due quadretti”.
Questa insicurezza ha spinto alcuni ragazzini a chiedersi: “Come possiamo verificare che l’espressione che abbiamo scritto sia giusta?”
In alcuni gruppi la verifica è stata fatta andando a sostituire nelle espressioni letterali i valori di n per i quali si fossero già trovate le risposte (n=3 e n=4).
Un altro modo per verificare la correttezza delle proprie risposte (a patto che nessuna di esse sia stata data “per differenza”) è quello di usare un conto prettamente algebrico. Infatti, se il ragionamento svolto e le espressioni letterali trovate sono corretti, si dovrebbe poter verificare che la somma dei cubetti con 3, 2, 1 e 0 facce colorate dà il numero totale di cubetti, cioè che:
(n – 2)3 + 6(n – 2)2 + 12(n – 2) + 8 = n3 .
I ragazzi più grandi, che abbiano studiato anche il cubo di un binomio, potranno riconoscere in questa identità la relazione:
(n – 2)3 + 6(n – 2)2 + 12(n – 2) + 8 = ((n – 2) + 2)3 = n3 .
Ma anche senza bisogno di conoscere i prodotti notevoli, è sufficiente la proprietà distributiva (e un po’ di pazienza) per verificare questa uguaglianza.
Durante la discussione finale, a nostro parere, l’insegnante dovrà sottolineare come positivo l’atteggiamento di chi cerca un modo per verificare la correttezza delle proprie risposte e cercherà di stimolare questo atteggiamento se non fosse già presente nei ragazzi della propria classe. Più i ragazzi sono maturi, più si potrà anche discutere con loro del fatto che queste verifiche non ci danno la certezza assoluta della bontà delle nostre risposte: se la verifica non torna, sappiamo di aver sbagliato da qualche parte, ma non sappiamo dove (paradossalmente, potremmo aver sbagliato la stessa verifica); e se la verifica torna, potrebbe essere un caso, o potrebbe essere l’effetto di un errore che si somma ad un altro errore.
Pur con questa consapevolezza, prendere l’abitudine di verificare i risultati ottenuti, nel senso non soltanto di rivedere calcoli e passaggi, ma di guardare le cose da un diverso punto di vista è utile e opportuno e non costituisce affatto una perdita di tempo. La fase di verifica di un problema non consente solo di controllare se il risultato è giusto o sbagliato: permette spesso di giungere ad una sua più profonda comprensione, di scoprire legami e relazioni prima nascosti. Non sappiamo dirlo meglio che usando le parole di George Polya (Come risolvere i problemi di matematica, UTET):
Per convincersi dell’esistenza oppure della qualità di un oggetto è necessario vederlo oppure toccarlo. E, come ogni percezione è più precisa se confermata da due sensi distinti, così è preferibile trarre la certezza da due prove diverse.
verso i casi limite
Alcuni gruppi di ragazzi potrebbero domandarsi perché siamo partiti da n=3 e abbiamo poi considerato numeri n>3; e potrebbero voler esaminare che cosa succede quando n=2. Dovrebbero rendersi conto abbastanza facilmente che restano gli 8 cubetti con tre facce colorate, in corrispondenza dei vertici, e nient’altro; e potrebbero ritrovare questo fatto anche dal punto di vista algebrico: infatti n-2=0.
A dirla tutta, molti dei gruppi ai quali è stato proposto questo problema sembrano non aver nemmeno letto l’inciso che nel testo dice che n deve essere maggiore di 2, al punto che spesso per rispondere alla domanda “Quanti cubetti hanno più di tre facce rosse?” scrivono “Nessuno, tranne nel caso in cui n=1″, dimostrando, con questa risposta, di non avere la pazienza di leggere attentamente un testo, ma di avere invece un buono spirito di immaginazione tridimensionale!
verso il coding
Il problema può essere ampliato anche nell’ottica del pensiero computazionale: si tratta di dare istruzioni semplici e precise affinché chiunque (anche una macchina, che non può prendere iniziative) possa calcolare, per un numero qualsiasi di suddivisioni dello spigolo del cubo, quanti cubetti di ciascun tipo si ottengono.
Volendo, si può proseguire con una attività di coding, ossia chiedere ai ragazzi di tradurre queste istruzioni in un linguaggio che possa essere compreso da un certo programma per il computer, piuttosto che da una certa applicazione o da una calcolatrice.
Nell’immagine seguente sono evidenziate le istruzioni che possono essere date al foglio elettronico Fogli Google, disponibile gratuitamente on-line.
Un problema difficile
Questo problema, che come struttura sembra essere molto simile ad Affettare un quadrato ed Affettare un triangolo, ha in realtà un grado di difficoltà in più: mentre in quei problemi il numero di quadratini o di triangolini di ciascun tipo poteva essere, nei casi particolari analizzati, contato direttamente sulla figura, in questo problema (che ha a che fare con una figura tridimensionale) ci sono dei cubetti che, nel disegno, rimangono nascosti.
In altre parole, il conteggio delle parti in cui è diviso il cubo, anche nei casi particolari, non può essere effettuato direttamente sulla figura. O meglio: si può effettuare un conteggio diretto solo se si dispone (al posto del disegno del cubo) di un modellino tridimensionale. E se questo modellino tridimensionale non è “scomponibile”, i cubi interni (quelli con nessuna faccia rossa, per intenderci) rimangono comunque nascosti. C’è bisogno quindi, come già si metteva in evidenza, di avere chiara la “struttura” di un cubo.
Scenari possibili
“Affettare un cubo”, nella formulazione con la quale è qui pubblicato, è un problema sfidante per ragazzini delle classi terze della scuola secondaria di primo grado, ma anche per ragazzi del primo biennio di quella di secondo grado.
Ai bambini della scuola primaria potrebbe essere significativo proporre un problema simile, limitando le richieste al cubo i cui spigoli sono divisi in 3 o in 4 parti uguali e fornendo loro alcuni modellini.
In questo caso, sarebbe interessante vedere se i ragazzini si limitano a contare i cubetti “uno a uno” o se (magari stimolati dall’insegnante, che può invitarli a trovare un modo sicuro “per non perdere il conto”) riescono a trovare il legame con il numero di vertici, facce e spigoli del cubo.
Materiale necessario
Potrebbe essere utile per i ragazzi avere qualche cubo da sovrapporre (non necessariamente da poter colorare), per poter formare un cubo più grande.
La carta isometrica e la carta a quadretti possono essere entrambe utili per disegnare una rappresentazione bidimensionale del cubo.
Volendo ampliare il discorso verso l’avvio al pensiero computazionale, potrebbe essere interessante mettere a disposizione dei ragazzi un foglio di calcolo o una calcolatrice programmabile, a seconda di quale strumento sono eventualmente abituati ad utilizzare.
Problema tratto da…
Affettare un cubo è tra i Problemi per matematici in erba citati in Diario di bordo (Sofia Sabatti, edizioni mateinitaly, 2020) un testo nel quale alcuni dei problemi presentati in questo sito vengono contestualizzati all’interno di un anno scolastico vissuto da una classe terza della scuola secondaria di primo grado.
Problemi collegati
Affettare un quadrato è una variante più semplice di questo problema. Anche Affettare un triangolo è analogo a questo: per un verso è più semplice perché il problema resta bidimensionale, per un altro verso è più complicato perché richiede delle strategie di conteggio che possono essere meno evidenti.