Biancaneve divide tra i sette nani il suo raccolto di 77 funghi.
Comincia a servire il più piccolo, Cucciolo, e poi di seguito serve tutti gli altri: Mammolo, Brontolo, Eolo, Dotto, Gongolo e Pisolo.
Ogni nano riceve un fungo in più di quello che l’ha immediatamente preceduto e Biancaneve riesce così a distribuire tutti i funghi raccolti.
Leggi tutto “Biancaneve e i 77 funghi”
Poligoni regolari e frazioni: un po’ più di varietà
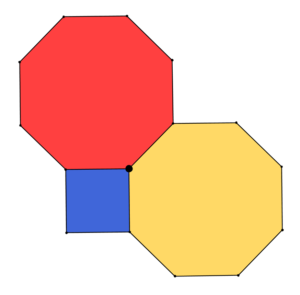
Nella figura qui sotto vedete tre poligoni regolari, due ottagoni e un quadrato, che hanno in comune un vertice e che riempiono perfettamente, senza sovrapposizioni e senza buchi, l’angolo giro intorno a quel vertice.
Riccardo, che in questo periodo sta studiando le frazioni, vedendo la figura su un libro, esclama “To’! Nella figura riesco a vedere che 3/8 + 3/8 + 1/4 = 1”.
Leggi tutto “Poligoni regolari e frazioni: un po’ più di varietà”
Allegati
Le tre piramidi e il cubo
Per condividere con gli alunni il video che presenta questo problema, fornire il seguente link:
https://youtu.be/-YKYb50LzY8
Soluzione
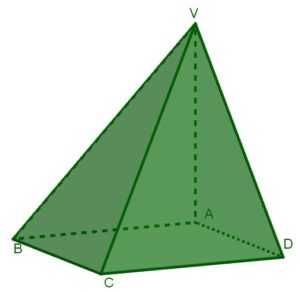
Ciascuna piramide ha 5 facce: un quadrato, due triangoli rettangoli isosceli uguali tra loro e altri due triangoli rettangoli uguali tra loro.
Ciascuna piramide ha 8 spigoli e 5 vertici.
Se lo spigolo del cubo che si ottiene unendo le tre piramidi misura 7 cm, le misure richieste nel problema (facendo riferimento alla figura qui sopra) sono le seguenti:
- i segmenti AB, BC, CD, DA, AV sono tutti spigoli del cubo e quindi misurano 7 cm;
- i segmenti BV e DV sono diagonali delle facce del cubo e misurano 7√2 cm (ossia circa 9,9 cm);
- il segmento CV è la diagonale del cubo e quindi misura 7√3 cm (ossia circa 12,1 cm);
- l’area della base ABCE misura 49 cm2;
- l’area dei triangoli rettangoli isosceli ABV e ADV misura 24,5 cm2;
- l’area dei triangoli rettangoli BCV e DCV misura 24,5√2 cm2;
- il volume della piramide misura 49×7/3 cm3=343/3 cm3 ossia circa 114,3 cm3.
Lo sviluppo piano della piramide descritta può essere rappresentato in modi diversi, ad esempio:
Se indichiamo con s la misura dello spigolo del cubo che si ottiene unendo le tre piramidi, le misure richieste nel problema (facendo riferimento alla figura qui sopra) sono le seguenti:
- i segmenti AB, BC, CD, DA, AV hanno lunghezza s;
- i segmenti BV e DV misurano √2s;
- il segmento CV misura √3s;
- l’area della base ABCE misura s2;
- l’area dei triangoli rettangoli isosceli ABV e ADV misura s2/2;
- l’area dei triangoli rettangoli BCV e DCV misura s2√2/2;
- il volume della piramide misura s3/3.
Commenti
Un problema significativo
“Le tre piramidi e il cubo” permette, manipolando e osservando oggetti molto semplici, di avvicinarsi ad alcuni fatti della geometria solida elementare che tanto elementari non sono.
Per prima cosa, il problema fornisce un esempio concreto di piramide che (pur essendo una semplicissima piramide a base quadrata) è diversa da quelle che fanno parte dell’immaginario collettivo (come le piramidi d’Egitto) e che sono piramidi rette (ossia piramidi nelle quali il piede dell’altezza cade nel centro della circonferenza inscritta nel poligono di base). È buffo vedere come nei libri di testo della scuola media non si lavori mai su piramidi che non siano rette!
In secondo luogo, il problema permette di visualizzare la diagonale del cubo e la diagonale delle facce del cubo. Un altro modello molto utile a questo scopo è quello dello “scheletro” di un cubo costruito, per esempio, con cannucce e scovolini da pipa.
Inoltre questo problema rende visibile, in un caso particolare, il fatto che il volume di una piramide è 1/3 del volume di un parallelepipedo con lo stesso poligono di base e la stessa altezza. Non si tratta di una dimostrazione, chiaramente: è però un buon modo per convincere i ragazzi del fatto che la “formula” che trovano sul libro è plausibile e per rendere quella stessa formula più facile da memorizzare.
Metacognizione
“Le tre piramidi e il cubo” insegna, a proposito dell’apprendimento, che a volte possiamo conoscere meglio qualcosa scomponendolo in parti o, viceversa, componendo parti più semplici a formare un tutt’uno più complesso.
Questa abilità del passare dalla parte al tutto (e viceversa) o da un problema a dei sotto-problemi (e viceversa) si costruisce nel tempo, anche affrontando problemi come questo, in cui la parte e il tutto sono oggetti concreti.
Un problema memorabile
Come si diceva poco sopra, è probabile che i ragazzi, dopo aver toccato con mano le tre piramidi e il cubo che esse formano, ricordino più facilmente il fattore 1/3 nella formula che lega il volume della piramide all’area di base e all’altezza.
Un problema aperto
Una delle direzioni verso le quali è possibile proseguire il discorso aperto da “Le tre piramidi e il cubo” è quella dell’avvio all’algebra.
Nel video viene chiesto ai ragazzi più grandi (immaginiamo quelli della classe terza della scuola secondaria di primo grado, ma tutto dipende dal livello di confidenza raggiunto nell’uso delle lettere come numeri) di esprimere le lunghezze degli spigoli e le aree delle superfici delle facce della piramide in funzione della misura s dello spigolo del cubo.
A meno che i ragazzi abbiano già imparato a memoria eventuali formule presenti sul libro di testo, la cosa più difficile è manipolare l’algebra che permette di determinare, applicando il teorema di Pitagora, le misure della diagonale del quadrato e della diagonale del cubo.
La misura della diagonale BV della faccia del cubo è data da
√(s2+s2)=√(2s2)=√2·√s2=√2·s
La misura della diagonale CV del cubo è data da
√(s2+(√2·s)2)=√(s2+2s2)=√(3s2)=√3·√s2=√3·s.
Se i ragazzi da soli non riuscissero in questa “impresa”, vale la pena di accompagnarli, perché questo calcolo (se non lo si fa diventare un mero esercizio di tecniche imparate a memoria) permette di ritornare sulla definizione di radice quadrata e sul suo significato.
È esperienza comune di noi insegnanti, infatti, quella di ragazzini (e non solo ragazzini!) che sanno calcolare la radice quadrata di quadrati perfetti grandissimi, o sanno approssimare la radice quadrata dei numeri più strani (usando le tavole numeriche, la calcolatrice, o qualche algoritmo imparato più o meno a fatica), ma poi non sanno rispondere a domande come “qual è il quadrato di √3?” o che, per rispondere a domande tipo “qual è la radice quadrata del quadrato di 57?” prima calcolano il prodotto di 57×57 e poi estraggono la radice quadrata.
Trovare l’area delle facce della piramide non dovrebbe creare grosse difficoltà:
- il quadrato di base ha area s2;
- le facce a forma di triangolo rettangolo isoscele sono metà quadrato, quindi hanno area s2/2;
- le altre due facce hanno ciascuna area
(s·√2·s)/2=(√2·s2)/2.
Nelle classi in cui abbiamo proposto questo problema è stato interessante chiedere l’area totale della superficie dello sviluppo piano della piramide. Si è infatti creata l’occasione per rispondere, con un esempio, a una domanda pressante da parte dei ragazzi: a che cosa serve il calcolo letterale? L’espressione che si ottiene applicando la proprietà distributiva alla somma delle singole aree è questa:
(2+√2)s2.
I ragazzi vedono immediatamente che questa espressione, anche se ha richiesto un po’ di “lavoro con le lettere” è più facile da gestire (ad esempio se chiediamo ai ragazzi di disegnarne il grafico o di farlo disegnare ad un foglio di calcolo) rispetto a quella “non semplificata”:
s2+2·(s2/2)+2·(√2·s2)/2.
Inoltre è interessante notare, insieme ai ragazzi, che le due espressioni possono essere entrambe utili per capire cose diverse: se la prima dice immediatamente che la misura della superficie dello sviluppo piano della piramide dipende solo dallo spigolo di base ed è direttamente proporzionale al suo quadrato, la seconda è di lettura meno immediata, ma può essere utile per mettere in evidenza l’area delle singole facce della piramide.
Un problema di matematica con effetto sorpresa
Nel video l’effetto sorpresa è “vanificato” dal fatto che il cubo viene mostrato presto. Ma può essere riconquistato facendo effettivamente costruire ai ragazzi le tre piramidi (una volta scoperto come deve essere lo sviluppo piano) e lasciando che essi chiedano ad amici e parenti se riescono a ricostruire, con esse, un cubo.
Scenari possibili
Il problema è, nel suo complesso, particolarmente adatto alle classi terze della scuola secondaria di primo grado o alle classi prime della scuola secondaria di secondo grado.
Evitando di indugiare sulla domanda che richiede un minimo di confidenza con l’uso delle lettere per esprimere numeri, può essere però anche molto adatto per una classe seconda media, come problema in cui si vede concretamente applicato, in modo significativo, il teorema di Pitagora.
E ancora: se ci si limita alla prima richiesta (contare i vertici e gli spigoli e descrivere la forma delle facce) può essere proposto anche a classi prime della scuola secondaria di primo grado o ad alunni della scuola primaria.
Materiale necessario
Nel caso in cui si chieda ai ragazzi di costruire le piramidi, sono necessari cartoncino, materiale da disegno, forbici e nastro adesivo.
Problema tratto da…
Le tre piramidi e il cubo è tra i Problemi per matematici in erba citati in Diario di bordo (Sofia Sabatti, edizioni mateinitaly, 2020), un testo nel quale alcuni dei problemi presentati in questo sito vengono contestualizzati all’interno di un anno scolastico vissuto da una classe terza della scuola secondaria di primo grado.
Affettare un cubo
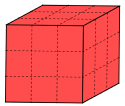
Partiamo da un cubo, coloriamone la superficie esterna di rosso e affettiamolo in cubetti, dividendo ogni spigolo in tre parti uguali, come in figura.
Siete d’accordo che i cubetti in totale sono 27 e che, fra questi, ce n’è uno solo (al centro) che non ha facce rosse, ce ne sono 6 con una sola faccia rossa, 12 con due facce rosse, 8 con tre facce rosse, e nessuno con più di tre facce rosse?
Leggi tutto “Affettare un cubo”
Allegati
Il patchwork quadrato
La nonna di Alessandra vuole confezionare una coperta quadrata, con la tecnica del patchwork, ossia unendo tramite cuciture tanti riquadri di stoffe diverse. Ha preparato 25 riquadri di stoffe di 5 colori diversi: 5 riquadri per ciascun colore.
Leggi tutto “Il patchwork quadrato”
Allegati
Affettare un triangolo
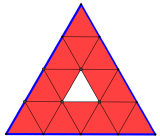
Partiamo da un triangolo equilatero e dividiamolo in triangolini, suddividendo ogni lato in un certo numero di parti uguali. In questa prima figura ogni lato è stato diviso in 4 parti uguali e si sono così formati 16 triangolini. La cornice colorata in rosso comprende tutti i triangolini che toccano (anche solo con un vertice) il contorno blu del triangolo di partenza ed è formata da 15 triangolini, mentre all’interno della cornice resta un solo triangolino.
Leggi tutto “Affettare un triangolo”
Allegati
C’è scatola e scatola
Alice e Vanessa sono sorelle e, come spesso accade, sono sempre molto attente a che una non riceva (da nonni, genitori o adulti in generale) qualche cosa in più dell’altra, che si tratti di attenzioni, di regali o del permesso di fare qualcosa.
Con grande gioia della mamma stanno mettendo in ordine la loro camera e vorrebbero avere una scatola per ciascuna, in cui mettere i propri braccialetti. Si mettono così a cercarle nell’armadietto dove sono riposte tutte le vecchie scatole vuote (di biscotti, di scarpe, di caffè, di cioccolatini…), ma dopo poco nasce un litigio furibondo, perché non ne trovano due uguali.
Leggi tutto “C’è scatola e scatola”
Allegati
L’ultima cifra
La storia
L’altro giorno Chiara discuteva con due suoi amici; erano presenti anche Alberto, il cugino grande di Chiara, che studia ingegneria all’università, e sua zia, che fa la ricercatrice in matematica. Chiara è ancora alla scuola primaria, ed è una ragazzina sveglia a cui piace giocare con i numeri; prima ha detto ai suoi amici che lei (da vera maghetta) sa che 9x9x9x9x9 è un numero che finisce per 9; e fin qui tutti le han creduto, anche perché lo hanno verificato con la calcolatrice. Ma poi li ha addirittura sfidati in questo modo: Voi ditemi un numero, qualsiasi, anche grandissimo, e io vi so dire qual è l’ultima cifra di 9x9x… moltiplicando tanti 9 quanti ne indica il numero che mi avete detto. E se non è magia questa…!
Leggi tutto “L’ultima cifra”
Allegati
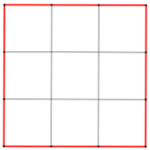
Affettare un quadrato
Partiamo da un quadrato, mettendone in evidenza i lati (in figura colorati in rosso); tagliamolo in quadratini, dividendo ogni lato in tre parti uguali; come vediamo dalla figura, dei 9 quadratini ottenuti, uno non ha lati rossi, 4 hanno un solo lato rosso, 4 ne hanno due e nessuno ne ha più di due.
Leggi tutto “Affettare un quadrato”