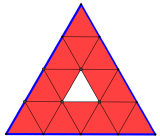
Partiamo da un triangolo equilatero e dividiamolo in triangolini, suddividendo ogni lato in un certo numero di parti uguali. In questa prima figura ogni lato è stato diviso in 4 parti uguali e si sono così formati 16 triangolini. La cornice colorata in rosso comprende tutti i triangolini che toccano (anche solo con un vertice) il contorno blu del triangolo di partenza ed è formata da 15 triangolini, mentre all’interno della cornice resta un solo triangolino.
Ora dividiamo un triangolo equilatero in triangolini suddividendo però ogni lato in 5 parti uguali, come in quest’altra figura. Quanti triangolini si sono formati? Da quanti triangolini è formata la cornice colorata in rosso, costruita con la stessa regola di prima? Quanti sono i triangolini bianchi all’interno della cornice?
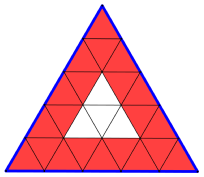
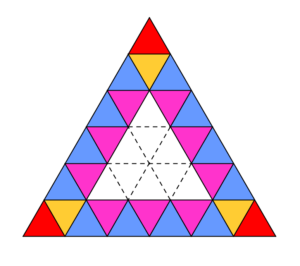
Dividiamo ora un triangolo equilatero in triangolini suddividendo però ogni lato in 6 parti uguali.
Quanti triangolini si sono formati?
Quanti triangolini ci sono nella cornice rossa?
Quanti triangolini bianchi ci sono all’interno della cornice?
E andando avanti? Se il lato del triangolo viene diviso in n parti uguali, possiamo dire quanti triangolini si sono formati, quanti sono i triangolini nella cornice rossa e quanti sono i triangolini bianchi all’interno?
Tenete presente che n è qui un numero intero, positivo, anche se… non sappiamo di che numero si tratta. Quindi le operazioni che dovrete indicare sul numero n per ottenere il numero totale dei triangolini (e il numero di quelli rossi o di quelli bianchi) dovranno “funzionare” per un numero n qualsiasi, purché n>3 (e il fatto che già sapete che cosa succede in alcuni casi, per esempio quando n=4 o n=5, può aiutarvi a controllare la correttezza della vostra risposta).
Soluzione
| Numero di parti in cui è diviso il lato | 5 | 6 | n |
| Numero di triangolini | 25 | 36 | n2 |
| Numero dei triangolini rossi | 21 | 27 | 6n-9 |
| Numero dei triangolini bianchi | 4 | 9 | (n-3)2 |
Commenti
Non dovrebbe essere troppo difficile arrivare a immaginare che il numero totale di triangolini è n2 (anche se sicuramente per i ragazzi non sarebbe semplice darne una motivazione chiara e comprensibile, che peraltro nel testo del problema non viene richiesta).
I ragazzi possono riconoscere la successione dei quadrati nella seconda riga di una tabella di questo tipo (e potranno farlo con tanta più facilità quanti più saranno gli esempi particolari che andranno a considerare):
| Numero di parti in cui è diviso il lato | 4 | 5 | 6 |
| Numero di triangolini | 16 | 25 | 36 |
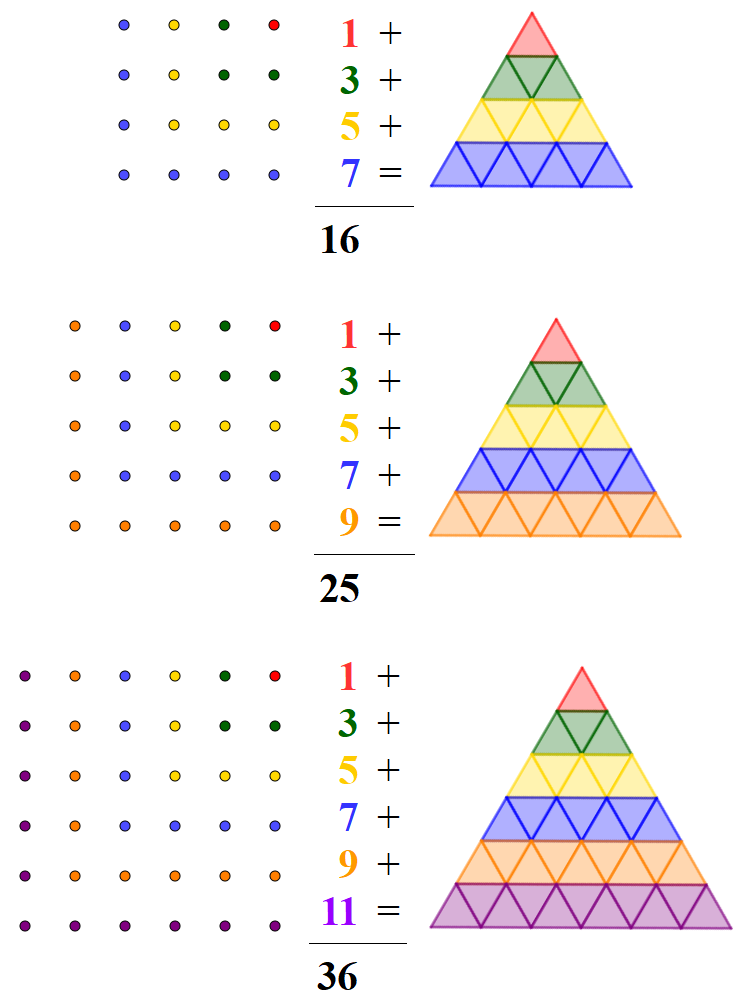
Qualcuno potrebbe invece contare i triangolini “riga per riga” e accorgersi che in ogni riga c’è un numero dispari di triangolini: due in più rispetto a quelli della riga precedente. Il numero totale dei triangolini presenti in un triangolo formato da n righe è quindi uguale alla somma dei primi n numeri dispari.
Una giustificazione formale del fatto che questa somma sia proprio uguale a n2 (si potrebbe fare, per esempio, per induzione, ma) è naturalmente al di fuori della portata dei ragazzi; tuttavia, immaginando di visualizzare i numeri quadrati come facevano gli antichi Greci, si può dare un forte supporto grafico intuitivo a questa affermazione.
Un inciso: questo è un classico esempio di “proof without words“, come vengono chiamati nel mondo anglosassone alcune figure o diagrammi che aiutano a convincersi del fatto che una particolare affermazione matematica sia vera. Potremmo chiamarla una “dimostrazione grafica”? Che ne pensate?
Ragionando in questo modo si ottiene così anche, quasi in automatico, che il numero dei triangolini nel triangolo interno è… la stessa cosa con il lato diviso in (n-3) parti uguali e quindi (n-3)2. A questo punto il numero di triangolini della cornice può essere ottenuto per differenza: n2– (n-3)2 e, volendo, si può anche dire che questa espressione equivale a 6n-9.
Strategie risolutive diverse
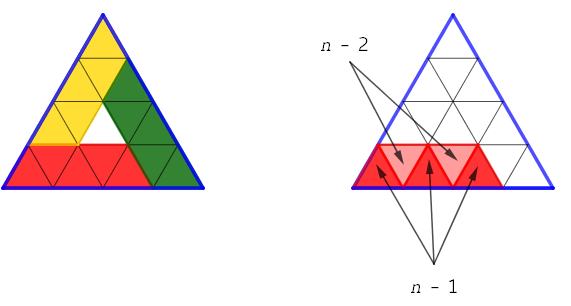
Si potrebbe anche cercare di contare direttamente i triangolini della cornice e sono diverse le strategie che potrebbero essere messe in campo. La figura qui sotto dà l’idea di come si possa spezzare la cornice in tre trapezi, ciascuno dei quali è composto da (n-1)+(n-2) = 2n-3 triangolini. In totale quindi si trovano proprio i 6n-9 triangolini della cornice.
Oppure si potrebbero contare i triangolini della cornice, distinguendoli a seconda di che cosa hanno in comune con il bordo esterno del triangolo.
Facendo riferimento alla figura (per il caso n=6), ci sono:
- 3 triangolini (rossi in figura) che hanno in comune con il bordo esterno due lati; e questi sono sempre 3, qualunque sia n;
- 3 triangolini (gialli in figura) che hanno in comune con il bordo esterno due vertici; anche questi sono sempre 3, qualunque sia n;
- alcuni triangolini (azzurri in figura) che hanno in comune un lato con il bordo esterno: questi sono n-2 per ciascun lato del triangolo grande e quindi 3n-6 in totale;
- alcuni triangolini (viola in figura) che hanno in comune solo un vertice con il bordo esterno: questi sono n-3 per ciascun lato del triangolo grande e quindi 3n-9 in totale.
In tutto abbiamo contato 3 + 3 + (3n-6) + (3n-9) = 6n-9 triangolini, come già avevamo trovato.
Naturalmente queste non sono le sole possibilità e i ragazzi potrebbero anche stupirvi immaginando altre maniere corrette per arrivare allo stesso risultato.
Un problema aperto
Confrontare e verificare le soluzioni
Nel testo di questo problema non abbiamo inserito una esplicita richiesta di motivazione; nella discussione, però, potrebbe sorgere la necessità di trovare delle giustificazioni.
Può essere l’insegnante, a chiedere dei “Perché?” ai suoi studenti. Ma, immaginando che il problema venga discusso in un lavoro di gruppo, pensiamo che queste richieste possano emergere in maniera naturale anche dagli alunni. Se i ragazzi sono sufficientemente motivati, probabilmente non si limiteranno ad accogliere una risposta qualsiasi di un loro compagno, ma vorranno capire da dove viene questa risposta. E questo sarà ancor più vero se ai ragazzi toccherà confrontarsi su risposte diverse per capire chi ha ragione.
In questi casi, soprattutto da ragazzini della scuola media, non possiamo certo aspettarci una giustificazione rigorosa ed espressa in un linguaggio ineccepibile: sarà l’insegnante a decidere, di volta in volta, se un “tentativo di giustificazione” è accettabile o meno. Il criterio che ci sembra opportuno suggerire è quello della comprensibilità: l’esigenza della giustificazione nasce dalla discussione fra compagni e abbiamo bisogno quindi che quello che dice uno venga compreso dagli altri.
studiare i casi n=1, n=2 e n=3
Alcuni gruppi di ragazzi potrebbero domandarsi perché siamo partiti da un numero n>3, e potrebbero voler esaminare i tre casi iniziali. Vale anche per n=1, n=2 e n=3 il fatto che il numero totale di triangolini è n2; vale per n=3 ma non per n=1 o n=2 il fatto che i triangoli bianchi all’interno (nessuno, in tutti e tre i casi) sono (n-3)2 e il fatto che i triangoli rossi siano 6n-9.
Scenari possibili
Come accennato più sotto, su questo sito si trovano anche altri problemi che possono essere ben sfruttati per un avvio all’algebra a partire da configurazioni geometriche interessanti e non banali.
Se lo “spirito” di questi problemi è il medesimo (scoprire il numero dei componenti di certe figure in funzione di un certo numero su cui si basa la costruzione della figura stessa, in questo caso il numero di parti in cui si divide il lato del triangolo), il loro grado di difficoltà può essere molto diverso.
In particolare “Affettare un triangolo” ci pare più adatto a ragazzi di terza media o del biennio della scuola superiore, che ad alunni più giovani.
Immaginare le tre funzioni richieste (trovando poi una giustificazione alle proprie ipotesi) a partire da una tabella in cui gli alunni abbiano riportati i valori ottenuti nei casi particolari non è certo immediato.
Scoprire le medesime funzioni osservando i disegni è possibile (e, come abbiamo visto, è possibile in tanti modi diversi), ma richiede l’abilità di immaginare la figura data scomposta in tante figure diverse, in una maniera che per molti potrebbe risultare più innaturale rispetto ad altre decomposizioni. Ad esempio: “vedere” che, dividendone il lato in n parti uguali, un quadrato si decompone in n2 quadratini (che è la decomposizione presentata nel problema Affettare un quadrato) è sicuramente più immediato e naturale rispetto a “vedere” che anche un triangolo si decompone allo stesso modo in n2 triangolini.
Controllare che i vari modi eventualmente utilizzati nei diversi gruppi per contare i triangolini portino allo stesso risultato richiede poi di accorgersi del fatto che le tre espressioni
-
- n2-(n-3)2
- 3[(n-1)+(n-2)]
- 3+3+3(n-2)+3(n-3)
(o altre che gli alunni potrebbero ottenere contando i triangolini della cornice in modi ancora diversi da quelli presentati qui sopra) sono del tutto equivalenti.
Certamente è più facile e naturale affrontare un tale confronto dopo che già si sia familiarizzato con il problema di manipolare le espressioni letterali (e quindi non prima della terza media).
Tutto questo non toglie che si possa proporre “Affettare un triangolo” anche in una prima o in una seconda media: saremmo curiosi di leggere, nei commenti, le impressioni di altri insegnanti ed, eventualmente, di sapere come è andata nelle classi in cui il problema è stato proposto!
Materiale necessario
Può essere utile tenere a disposizione dei ragazzi qualche foglio di carta già divisa in triangolini (carta isometrica), in modo che si possano fare tante figure in maniera più spedita. La carta isometrica è scaricabile in un file formato pdf facilmente stampabile e fotocopiabile a fondo pagina.
Problema tratto da…
Affettare un triangolo è tra i Problemi per matematici in erba citati in Diario di bordo (Sofia Sabatti, edizioni mateinitaly, 2020) un testo nel quale alcuni dei problemi presentati in questo sito vengono contestualizzati all’interno di un anno scolastico vissuto da una classe terza della scuola secondaria di primo grado.
Problemi collegati
Per certi versi analoghi a questo possono essere considerati i problemi Affettare un quadrato e Affettare un cubo.



Questo è il genere di giochi che adoro! Mi piace fare con i miei alunni “i matematici che cercano formule meravigliose” come dico con loro! E a loro brillano gli occhi quando sentono di aver scoperto delle formule matematiche. Appena possibile lo sperimento! Grazie!
Grazie, Simona! Evviva la meraviglia dei nostri alunni di fronte alle loro scoperte matematiche!