Nella figura qui sotto sono rappresentati quattro sviluppi di un cubo. Potete immaginare di ritagliare ciascuno sviluppo e ripiegarlo in modo da ottenere un cubo.
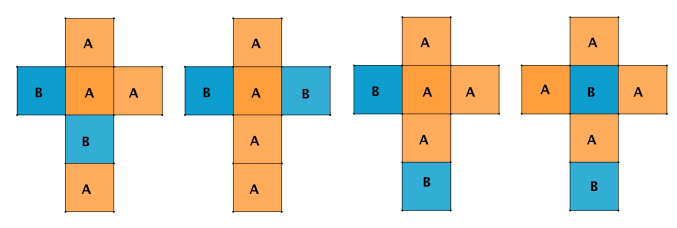
Come sono questi 4 cubi: uguali o diversi?
Tutti hanno 4 facce arancione (A) e 2 facce blu (B): ma sono colorati alla stessa maniera?
Quanti cubi colorati in maniera diversa trovate fra questi 4?
E, secondo voi, è possibile colorare un cubo con 2 facce blu e 4 arancione, in una maniera che sia diversa da tutte quelle rappresentate negli sviluppi qui sopra?
Noi diciamo che due cubi sono colorati alla stessa maniera se possiamo rigirare in mano uno dei due in modo che appaia proprio allo stesso modo dell’altro.
Gli sviluppi sembrano tutti diversi; attenzione, però! Può succedere che due sviluppi siano colorati in maniera diversa ma, quando li andate a richiudere, i due cubi siano proprio uguali!
Se pensate che vi possa aiutare, potete fare qualche prova ritagliando uno sviluppo di carta e ripiegandolo.
Soluzione
Ci sono solo due maniere diverse per colorare un cubo con 4 facce di un colore (A) e 2 di un altro colore (B), perché ci sono solo due possibili reciproche posizioni per due facce di un cubo (le due facce del colore B): possono essere parallele oppure toccarsi lungo uno spigolo.
Commenti
Il problema mira a mettere in gioco la capacità di immaginazione e visualizzazione dei ragazzi: a partire dallo sviluppo dovrebbero riuscire a immaginare il cubo tridimensionale, e la maniera in cui è colorato.
Si è detto che ci sono solo due maniere diverse per colorare un cubo con 4 facce arancione e 2 blu, perché ci sono solo due possibili reciproche posizioni per due facce di un cubo. Questo significa che:
- se abbiamo in mano due cubi, entrambi con due facce parallele blu e le altre arancione, riusciamo a rigirarli in modo che appaiano esattamente allo stesso modo;
- lo stesso accade se in entrambi i cubi le due facce blu sono adiacenti;
- se invece in uno dei due cubi le facce blu sono parallele e nell’altro sono adiacenti, non sarà mai possibile, neanche rigirandoli in qualunque modo, farli apparire identici.
Si tratta quindi di “vedere” dagli sviluppi che, riferendoci alla figura iniziale, nel primo e nel terzo cubo le due facce blu si toccano lungo uno spigolo mentre nel secondo e nel quarto sono parallele. Quindi, fra i cubi in figura, ci sono entrambi i tipi di colorazione e non se ne possono trovare altri che non siano rappresentati in figura.
Fra le possibili motivazioni che possono dare i ragazzi, ci sembrano valide tutte quelle che, sia pure in modo confuso e non tanto adeguato, fissino l’attenzione sulla reciproca posizione delle due facce blu (parallele o adiacenti).
Fra le possibili difficoltà e confusioni in cui incorreranno, è facile prevedere che uno scoglio sarà quello del passaggio dallo sviluppo piano all’oggetto tridimensionale: incoraggiateli a costruire un modellino, se lo ritengono utile.
Un problema aperto
Questo problema mette in evidenza come sviluppi piani colorati in modi diversi si possano richiudere in oggetti tridimensionali identici.
Una domanda che potrebbe nascere nei ragazzi, o che l’insegnante potrebbe in qualche modo stimolare, è questa: possono sviluppi piani diversi (non solo nel colore, ma proprio nella forma) originare oggetti tridimensionali uguali?
In particolare, potrebbe essere interessante lasciare che i ragazzi si cimentino nella ricerca dei possibili sviluppi piani del cubo. Raccolte le loro idee, uno dei seguenti strumenti può essere usato per illustrare e riassumere il tutto.
Un parquet cubistico
Il video raggiungibile cliccando sull’immagine qui sotto, prodotto in collaborazione con Sergei Petrovich Konovalov, è tratto dal sito Mathematical Etudes. “Un parquet cubistico” rappresenta gli 11 possibili sviluppi piani del cubo e come ciascuno di essi possa tassellare il piano.
nets of the cube
Nell’animazione raggiungibile cliccando sull’immagine qui sotto (costruita da Anthony OR 柯志明 del GeoGebra Institute of Hong Kong utilizzando GeoGebra), si possono vedere contemporaneamente gli undici “esamini” richiudersi a formare un cubo.
Sperimentazione e possibili scenari
Questo problema è stato sperimentato in 57 classi terze di docenti partecipanti ai corsi MathUp per la Scuola secondaria di primo grado nell’anno scolastico 2017 / 2018.
La maggior parte degli alunni di queste classi ha considerato le prime domande di “Quattro cubi” abbastanza facili, probabilmente anche perché hanno potuto costruire, in vario modo, dei modellini: qualcuno ha ritagliato e piegato la figura ricevuta insieme al testo; altri ragazzi hanno riprodotto gli sviluppi piani su cartoncino e hanno poi costruito i cubi; qualche gruppo ha disegnato (su carta a quadretti, in assonometria cavaliera) i cubi corrispondenti agli sviluppi dati; altri hanno usato il polydron [1].
Questi modellini hanno consentito a tutti di capire che a sviluppi piani “diversamente colorati” possono corrispondere cubi “ugualmente colorati”.
Ma poi gli stessi modellini sono stati utili soprattutto per rispondere all’ultima domanda del problema, ossia per andare alla ricerca di un eventuale terzo modo per colorare il cubo. È stata proprio su questa attività di esplorazione che si sono spesso concentrate le discussioni più accese tra i vari gruppi, conducendo la quasi totalità delle classi ad una risposta corretta e condivisa, espressa in modo chiaro anche se non sempre con linguaggio ineccepibile.
Il problema non richiede particolari strumenti matematici e inoltre il cubo è un solido con cui ben prima di arrivare in terza media i ragazzini hanno una gran familiarità: quindi il problema si può proporre anche ad alunni più giovani.
Materiale necessario
Cartoncino, colori e forbici possono servire per costruire dei modellini di cubi. Eventualmente si può partire da sviluppi piani costruiti col polydron e lasciare altri quadrati di polydron agli alunni perché ne costruiscano altri, ma non è affatto indispensabile.
Problema tratto da…
Questo problema è stato proposto tra i “problemi iniziali” della sperimentazione legata al corso MathUp per la classe terza della Scuola secondaria di primo grado nell’anno scolastico 2017 / 2018.
Problemi collegati
“Quattro cubi” è per molti versi simile al problema Sgabelli cubici.
Non si tratta di problemi identici: qui si passa per lo sviluppo piano dei cubi, al quale invece quel problema non rimanda; lì il numero di facce colorate con un certo colore può variare, mentre in questo ci sono esattamente due facce di un certo colore e le altre quattro di un altro. Identica però è la richiesta (distinguere tutti i tipi possibili di cubi diversamente colorati) e sicuramente simili sono i processi che i ragazzi dovranno mettere in atto per arrivare alla soluzione.
Assegnare prima uno dei due problemi e poi, a distanza di tempo, anche l’altro può essere un’occasione per verificare se e quanto del primo problema sia stato interiorizzato dai ragazzi.
Note
[1] Si tratta di uno strumento, come altri esistenti in commercio, che consiste di tessere poligonali di diverse forme, con la possibilità di incastrarle fra loro.




