Alice e Vanessa sono sorelle e, come spesso accade, sono sempre molto attente a che una non riceva (da nonni, genitori o adulti in generale) qualche cosa in più dell’altra, che si tratti di attenzioni, di regali o del permesso di fare qualcosa.
Con grande gioia della mamma stanno mettendo in ordine la loro camera e vorrebbero avere una scatola per ciascuna, in cui mettere i propri braccialetti. Si mettono così a cercarle nell’armadietto dove sono riposte tutte le vecchie scatole vuote (di biscotti, di scarpe, di caffè, di cioccolatini…), ma dopo poco nasce un litigio furibondo, perché non ne trovano due uguali.
Interviene allora la mamma, che in men che non si dica tira fuori dall’armadietto due scatole che le sembrano perfette: una ha la forma di un cubo, di spigolo 10 cm; l’altra ha forma di un parallelepipedo rettangolo e i suoi spigoli misurano uno 9 cm, uno 10 cm e l’altro 11 cm (la mamma è sarta e ha sempre in tasca un metro giallo e azzurro arrotolato, quindi fa prestissimo a prendere le misure).
Ovviamente Alice e Vanessa nel ricevere le scatole iniziano a lamentarsi: “La mia è più stretta!”, “La tua è più alta” e così via. Ma la mamma taglia corto: “Ma insomma… Uno spigolo ce l’hanno uguale; quello che manca al secondo è aggiunto al terzo, quindi a conti fatti le due scatole sono grandi uguali, anche se non hanno esattamente la stessa forma. Vedete? Adesso basta!”
Alice e Vanessa non sono convinte e continuano a discutere, dimenticandosi della buona idea che avevano avuto di mettere in ordine la camera.
E voi che ne dite?
È più grande il cubo che è toccato a Vanessa o l’altra scatola che è toccata ad Alice?
E, se Alice e Vanessa volessero ricoprire le loro scatole con una bella carta colorata autoadesiva, chi delle due avrebbe bisogno di più carta?
E se la mamma avesse dato ad Alice un’altra scatola, sempre a forma di parallelepipedo, con gli spigoli lunghi uno 10 cm, uno 8 cm e uno 12 cm, il volume di questa scatola sarebbe uguale, maggiore o minore rispetto al volume del cubo di Vanessa?
Come sono le superfici totali delle due scatole?
Sempre più difficile! Proviamo a generalizzare: confrontiamo un cubo di spigolo s (intendiamo con questa dicitura che s sia la misura dello spigolo, espressa in cm ) con un parallelepipedo rettangolo di spigoli
s–k, s e s+k
(le scatole di Alice e Vanessa corrispondevano ai dati di s=10 e k=1 oppure k=2).
Quale fra i due ha volume maggiore?
Quale ha superficie totale maggiore?
Riuscite a dare una stima a occhio prima di fare i conti?
Soluzione
Il volume della scatola di Vanessa è 1000 cm3 e la superficie totale è 600 cm2.
Il volume della scatola di Alice è 990 cm3 e la superficie totale è 598 cm2: quindi effettivamente la scatola di Alice è (un po’) più piccola di quella di Vanessa.
Il volume del cubo (espresso in cm3) è s3 e la superficie totale (espressa in cm2) è 6s2.
Il volume del parallelepipedo è s3 –sk2 che quindi è sempre minore di quello del cubo.
La superficie totale del parallelepipedo è 6s2 – 2k2 che quindi è sempre minore di quella del cubo.
Commenti
Scatole e parallelepipedi
La prima osservazione (doverosa…!) riguarda l’inevitabile scollamento che c’è tra la contestualizzazione proposta (le scatole) e la figura geometrica su cui i ragazzi faranno i conti (i parallelepipedi).
Ci sono almeno due questioni, al riguardo:
- le dimensioni “esterne” delle scatole (quelle da considerare per valutare quanta carta serve per ricoprirle) non sono uguali a quelle interne (che vanno prese in considerazione per valutare il volume utile); e la differenza può essere più o meno significativa, a seconda della scatola;
- alcune scatole (come quelle delle scarpe) sono dotate di un coperchio leggermente più grande del corpo della scatola, al quale in parte si sovrappone: può quindi sorgere il dubbio se vada rivestita anche la parte di scatola che rimane sotto il coperchio.
Se agli alunni queste problematiche non dovessero saltare all’occhio, si può inizialmente soprassedere (salvo poi eventualmente riprenderle a momento debito).
Ma se qualche alunno sollevasse una di tali questioni, varrebbe la pena valorizzare ed apprezzare la sua osservazione, oltre che e aiutare i ragazzi a mettersi d’accordo su come considerare volume e superficie.
Soprattutto sarebbe una bella occasione per far notare ai ragazzi come un problema di matematica possa costituire una modellizzazione di un problema “da vita quotidiana”. E, per ricavare da un problema reale un modello astratto, occorre consapevolmente ignorare alcuni dati e considerare solo quelli più significativi (e più significativi proprio per il particolare problema che abbiamo di fronte): quindi, nonostante spesso anche gli adulti definiscano la matematica “complicata”, il modello matematico è in generale più semplice (e spesso assai più semplice) rispetto al problema reale.
Tornando al problema proposto, questo potrebbe essere dato in poche righe:
“confrontare volume e superficie di un cubo di spigolo s con quelli di un parallelepipedo rettangolo di spigoli s–k, s e s+k“.
Rinunciare alla contestualizzazione scioglie naturalmente ogni tipo di ambiguità, ma implica anche rinunciare all’aiuto che la narrazione fornisce nel motivare i ragazzi e soprattutto nel dare significato a ciò di cui si sta parlando: troppo spesso i ragazzi sono abituati a trattare volume e superficie come formule magiche prive di senso reale (e magari addirittura intercambiabili…!).
Piuttosto, quindi, può valere la pena provare – magari con gli stessi alunni – a discutere di altre possibili contestualizzazioni, a cercare degli esempi di scatole, a valutare quali approssimazioni possono essere più o meno realistiche, rendendo così “C’è scatola e scatola” una situazione problematica sempre più ricca e sempre più aperta.
Soluzione nel caso s=10 e k=1
Per s=10 e k=1:
- il volume del cubo è 1000 cm3 e la superficie totale 600 cm2;
- 9x10x11= 990, quindi il volume del parallelepipedo è 990 cm3;
- 2x9x10 + 2x9x11 + 2x10x11 = 180 + 198 + 220 = 598, quindi la superficie totale del parallelepipedo è 598 cm2.
Quindi in questo caso il cubo ha sia volume che superficie totale maggiori di quelli del parallelepipedo.
Soluzione nel caso s=10 e k=2
Per s=10 e k=2:
- si è già trovato il volume e la superficie totale del cubo nel caso precedente;
- 8x10x12= 960 quindi il volume del parallelepipedo è 960 cm3;
- 2x8x10 + 2x8x12 + 2x10x12 = 160 + 192 + 240 = 592, quindi la superficie totale del parallelepipedo è 592 cm2.
Anche in questo caso il cubo ha sia volume che superficie maggiori di quelli del parallelepipedo.
Soluzione nel caso generale
Sottintendendo ovunque che i volumi sono espressi in cm3 e le superfici in cm2, si può dire che: il volume del cubo è s3 e la superficie totale 6s2.
Il volume del parallelepipedo è:
s(s+k)(s–k) = s3 –sk2 < s3.
La superficie totale del parallelepipedo è:
2(s(s+k) + s(s–k) + (s+k)(s–k)) = 2(3s2 – k2 ) = 6s2 – 2k2 < 6s2 .
L’intento di questa richiesta è duplice: da un lato c’è l’idea di far prendere la mano ai ragazzi su semplici espressioni algebriche, in situazioni nelle quali possa essere loro chiaro il significato di quello che stanno facendo; dall’altro ci piacerebbe che la curiosità rispetto alla generalizzazione possa sorgere dai ragazzi stessi (“La prima volta succede così, la seconda pure; ma allora succederà sempre così?“). Il fatto che ragazzi diversi possano avere, in merito a questo, idee diverse incoraggia la discussione. E da una tale discussione possono nascere tanti spunti positivi, sia dai ragazzi che hanno magari una bella capacità di visualizzazione geometrica e “lo vedono“, sia dall’algebra che mette la sua potenza al servizio di quelle intuizioni che altrimenti faticano a trovare una giustificazione.
Possibili scenari
Con i ragazzini più giovani, si può eliminare l’ultima richiesta, e chiedere quindi di esaminare solo i casi particolari (aggiungendone eventualmente altri). Alcuni casi possono anche venire visualizzati, costruendo cubo e parallelepipedo con cartoncino, polydron[1] o altro materiale.

Se però vogliamo utilizzare questo problema nell’ambito di un percorso di avvio all’algebra, allora sarà indispensabile provare a generalizzare. Ci sono varie strade possibili per proporre domande anche un po’ più semplici, ma che vadano sempre in questa direzione: per esempio, si può cominciare a proporre di studiare il caso di un cubo di spigolo 10 e un parallelepipedo di spigoli 10, 10+k, 10-k; oppure si può partire dal piano e chiedere ai ragazzi di confrontare area e perimetro di un quadrato di lato s con quelli di un rettangolo di lati s–k e s+k (anche in questo caso cominciando eventualmente da un quadrato di lato 10 e un rettangolo di lati 10+k e 10-k).
Materiale necessario
Costruire (o far costruire agli studenti) alcuni modellini relativi ad alcuni casi particolari, oppure mostrare (o far costruire agli studenti più esperti) una animazione, simile a quella realizzata con GeoGebra e qui sotto proposta, possono essere validi aiuti per immaginare la situazione 3d che il problema descrive. Teniamo sempre presente che la visualizzazione 3d è uno scoglio delicato, per affrontare il quale ognuno ha (consapevolmente o inconsapevolmente) strategie differenti.
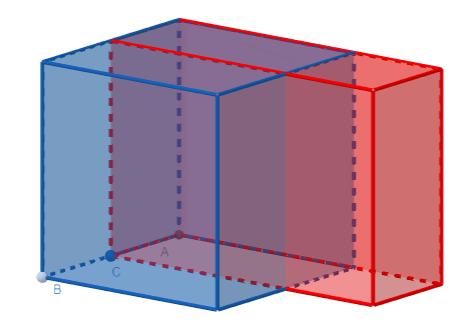
Nell’animazione raggiungibile cliccando sull’immagine qui sotto (costruita utilizzando GeoGebra), il cubo blu ha spigolo s; il parallelepipedo rosso ha altezza s e spigoli di base s–k e s+k; muovendo il punto B cambia il valore di s, muovendo il punto C cambia il valore di k.
Problema tratto da…
C’è scatola e scatola è tra i Problemi per matematici in erba citati in Diario di bordo (Sofia Sabatti, edizioni mateinitaly, 2020), un testo nel quale alcuni dei problemi presentati in questo sito vengono contestualizzati all’interno di un anno scolastico vissuto da una classe terza della scuola secondaria di primo grado.
Note
[1] Il polydron è uno strumento, come altri esistenti in commercio, che consiste di tessere poligonali di diverse forme, con la possibilità di incastrarle fra loro.



E’ un ottimo problema.
Per aiutare un pò quelli in difficoltà si potrebbe fornire il disegno dei solidi per visualizzare le dimensioni s-k, s, s+k?
Altra cosa: c’è tanto testo e dalla mia esperienza un discreto numero di alunni nel contesto ampio si perde le informazioni utili.
Si può pensare che il docente legga la presentazione e poi fornisca agli alunni una sintesi sulla quale i ragazzi poi lavorano?
La parte che chiede di calcolare la superficie come quantità di carta da usare è sempre un pò scollegata dalla realtà perché dipende dal foglio che hai a disposizione e in quale modo ritagli le varie facce, se una faccia può essere ricoperta da più pezzi … In questo caso si potrebbe porre questa domanda: ” Ciascuna bimba ha disposizione un foglio di carta 50x30cm, dopo che hanno ricoperto le facce delle scatole chi delle due avrà usato più carta?”
Grazie a voi.
Gisella
Cara Gisella,
ogni volta che proponiamo qualche bel problema in classe è opportuno avere in tasca degli “aiuti”, anzi molti aiuti, anche di diverso genere, in modo da poter scegliere sul momento, a seconda delle reazioni dei ragazzi, quale possa essere più “sbloccante” in quel dato contesto: se il disegno di alcuni casi particolari, oppure gli sviluppi da cui costruire qualche modellino di questi casi particolari, oppure un disegno dinamico in GeoGebra (o altro software di geometria dinamica) che rappresenti la situazione generale, o altro ancora.
Anche per le difficoltà di lettura e di comprensione del testo (affrontare le quali è una componente essenziale, e ineliminabile, del nostro insegnamento), dobbiamo avere in tasca degli “aiuti” per evitare che i ragazzi si perdano prima ancora di arrivare alla domanda matematica: leggere il problema insieme a loro, porre loro alcune domande, adottare tutte quelle strategie che ci vengono in mente (o che vengono in mente ai nostri alunni) per passare da una mera lettura del testo a una sua effettiva comprensione. Comprensione che può sì essere facilitata o manifestarsi attraverso una sintesi, ma anche attraverso un disegno, una tabella, o un grafico, meglio se prodotti dai ragazzi stessi, piuttosto che forniti direttamente dall’insegnante.
Circa l’ultimo problema che sollevi (la carta), certamente mettersi su un piano reale rende la situazione più complessa e ci piacerebbe che fossero i ragazzi a osservare che la risposta alla domanda “chi ha bisogno di più carta?” dipende da tanti fattori! Non è un caso, poi, che le domande nella parte finale si focalizzino solo su volume e superficie, concetti per costruire il significato dei quali è bene passare anche attraverso i braccialetti con cui riempire le scatole e la carta con cui ricoprirle, ma che certo sono ben più astratti.
Grazie anche a te: ogni commento è sempre importante e gradito,
Sofia