I viaggi di Gulliver

Soluzione

Se il rapporto di similitudine è 1/12, allora il rapporto tra i volumi di due oggetti simili è (1/12)³ .
Quindi il volume di una botte nel nostro mondo, corrispondente a quella lillipuziana da 0,28 litri, conterrà circa
0,28 litri · 12³ = 0,28 litri · 1728 = 483,84 litri.

L’area del nostro lenzuolo a due piazze è di
2,5 m × 3 m = 7,5 m² = 75000 cm².
L’area del lenzuolo lillipuziano sarà allora di 75000/144 cm² cioè di circa 520cm²; il lenzuolo inoltre corrisponderebbe a un rettangolo di lati (circa) tra i 20 cm e i 25 cm, quindi potrebbe andar bene come tovagliolo per Gulliver.

Commenti

Un problema significativo

Il rapporto tra le aree e i volumi di figure simili

I nodi attorno ai quali è costruito questo problema sono:

• il rapporto tra le aree di due figure simili,
• il rapporto tra i  volumi di due oggetti tridimensionali che siano fra loro simili,
• il legame esistente tra questi rapporti e il rapporto di similitudine (ossia il rapporto tra le misure lineari nelle due figure simili o nei due oggetti tridimensionali simili).
  

Si potrebbe pensare che per una classe nella quale questi temi siano già stati affrontati “I viaggi di Gulliver” sia un esercizio, più che un problema. O che sia un “problema” solo nel senso che bisognerà, per trovare la risposta alle domande, comprendere bene il testo nella sua complessità. “I viaggi di Gulliver” potrebbe essere allora proposto a distanza di tempo, per verificare quanto è rimasto della spiegazione dell’insegnante, quanto le conoscenze siano state davvero interiorizzate e acquisite in maniera stabile.

In classi, invece, dove non si sia ancora condotta una riflessione sistematica su questi fatti, potrebbe essere l’occasione per avviare una discussione sul tema, discussione che avrà probabilmente bisogno dell’intervento dell’insegnante per portare frutto.

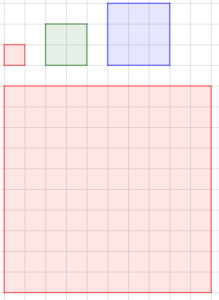
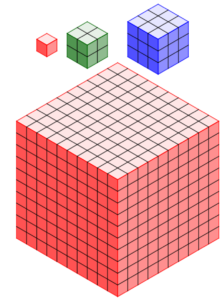
Facendoli riflettere su alcune figure, è facile convincere i ragazzi del fatto che, se due quadrati sono in rapporto di similitudine k (e quindi il lato del secondo è k volte il lato del primo), allora l’area del secondo è k² volte l’area del primo. È analogamente facile convincerli del fatto che, se due cubi sono in rapporto di similitudine k (e quindi lo spigolo del secondo è k volte lo spigolo del primo), allora il volume del secondo è k³ volte lo spigolo del primo.

Lo stesso ragionamento e un’analoga figura possono convincere facilmente del fatto che anche per due rettangoli o due parallelogrammi simili in rapporto di similitudine k (per i quali, quindi, ciascuno dei lati del primo è k volte il corrispondente lato del secondo) succede che l’area del primo è k² volte l’area del secondo. Così come, se due parallelepipedi sono simili, in rapporto di similitudine k, allora il volume del primo è k³ volte il volume del secondo.

Più difficile è far capire che il rapporto tra le aree di due figure simili qualsiasi è il quadrato del loro rapporto di similitudine e, analogamente, che il rapporto tra i volumi di due figure simili qualsiasi è il cubo del loro rapporto di similitudine.

Una possibile strada da percorrere in questa direzione è quella indicata nel capitolo “Che cos’è pi greco?” del libro La bellezza della matematica di Serge Lang (nella traduzione italiana edita in formato tascabile da Bollati Boringhieri nel 2015), che è possibile scaricare in fondo a questa pagina e da cui sono tratte le immagini seguenti.

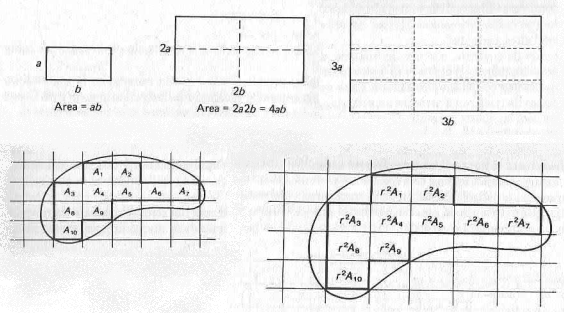
Le riflessioni che emergono dalla discussione di Lang con gli studenti della classe in cui avviene la lezione descritta possono essere così schematizzate:

• si riconosce innanzitutto che il rapporto tra le aree di due rettangoli simili è uguale al quadrato del loro rapporto di similitudine;
• si constata che l’area di una figura qualsiasi è riconducibile alla somma dell’area di tanti piccoli rettangoli (con eventualmente qualche passaggio al limite, sul quale l’insegnante valuterà l’opportunità di soffermarsi, a seconda della classe con la quale sta affrontando questo argomento); 
• si osserva che quando si dilata la figura di un fattore r, anche i rettangolini vengono dilatati dello stesso fattore r (e quindi la loro area si modifica secondo il fattore r²);
• si osserva che il numero dei rettangoli grossi nella figura dilatata è uguale al numero di rettangolini nella figura originale e si conclude quindi che l’area della figura dilatata è in rapporto r² con quella della figura originale, (così come l’area di un  rettangolo dilatato è in rapporto r² con l’area di un rettangolino).

Per seguire questo ragionamento non serve conoscere la “formula” per calcolare l’area della figura di cui si sta parlando e questo è un punto assai significativo in cui la proposta di Lang si differenzia da quanto proposto su quei pochi libri di testo di scuola media che affrontano questa questione.

Un discorso del tutto analogo può essere fatto anche per il volume, constatando così che il rapporto tra i volumi di due figure simili è uguale al cubo del loro rapporto di similitudine, come conseguenza del fatto che ciò avviene per i parallelepipedi e che, quando calcoliamo il volume di un solido qualsiasi, è un po’ come se contassimo tanti piccoli parallelepipedi in esso contenuti (somma  eventualmente portata al limite).
Anche nel caso del volume questo discorso vale per tutte le figure simili, comprese quelle delle quali non conosciamo la “formula” per il calcolo del volume (come accade per le botti).

Stimare il volume

L’errore classico in cui si “scivola” nell’affrontare questo problema sta nell’immaginare che, per ottenere il volume della botte nel nostro mondo, basti moltiplicare per 12 il volume della botte lillipuziana, ottenendo

0,28 litri · 12 = 3,36 litri.

In una delle classi in cui è stato proposto “I viaggi di Gulliver”, questo risultato, da alcuni alunni accettato senza fare una piega, ha fatto insorgere altri compagni, che si ricordavano di essere stati in gita scolastica in una fattoria e di aver visto delle botti vere. Alcuni di questi alunni, pur non avendo idea di come procedere per calcolare il volume della botte nel nostro mondo, erano certi che questo non potesse essere il risultato corretto, perché la botte che ricordavano era decisamente più voluminosa di due o tre bottiglie!

Obiezioni di questo genere sono estremamente preziose, se colte all’interno dei gruppi di lavoro o della classe intera, perché danno all’insegnante l’occasione di sostenere l’atteggiamento di coloro che non accettano passivamente un risultato, ma si chiedono se sia plausibile oppure no alla luce di una stima (consapevole o inconsapevole) fatta a priori.

Un problema difficile

Le difficoltà di comprensione del testo

La prima difficoltà che gli alunni potrebbero incontrare nell’affrontare questo problema è quella della comprensione del testo che lo introduce. Lo scopo della narrazione non è certo quello di complicare la vita degli studenti: semmai si prefigge il contrario, creando un contesto entro il quale possa essere più facile immaginarsi gli oggetti di cui si parla e le relazioni tra essi.

Questa facilitazione sussiste, però, solo per quei ragazzi che abbiano in qualche modo idea di chi sia Gulliver e di che mondo sia Lilliput (nonché di che cosa sia una botte): a chi non ha già questi riferimenti sarà opportuno dare modo di costruirseli, attraverso un libro illustrato, lo spezzone di un video, la lettura di una parte un po’ più lunga del romanzo, l’ascolto di una delle tante canzoni che dai viaggi di Gulliver hanno preso spunto.

Lo scoglio percettivo

Il legame che sussiste tra il rapporto di similitudine di due figure solide e quello dei loro volumi non è facile da intuire, forse anche per una questione percettiva.

Le due ciotole nella fotografia qui sopra sono simili, in rapporto di similitudine 1:2. Eppure, se non pensiamo bene a come stanno le cose, facciamo fatica a immaginare che il rapporto tra i loro volumi sia 1:8. In altre parole: è ben difficile che si arrivi a dire che il rapporto tra i volumi è 1:8 solo sulla base della nostra intuizione, solo sulla base di ciò che vediamo “a occhio”, senza fare ricorso alle nostre conoscenze di geometria.

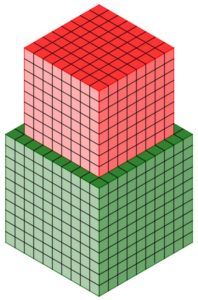
Analogamente, è difficile intuire a prima vista che il volume del cubo verde disegnato qui sotto è circa il doppio di quello del cubo rosso che gli è sovrapposto!

L’altezza del flacone di shampoo più grande tra quelli nella figura qui sotto è 24 cm e quella dei due più piccoli, del tutto simili al primo, è 18 cm. Anche in questo caso, stentiamo a credere che il contenuto dei due flaconi più piccoli ci stia in quello più grande.

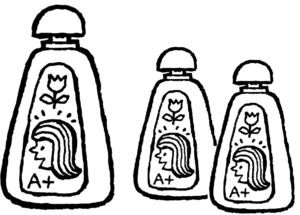
A cosa è dovuta questa difficoltà così diffusa?

Un’ipotesi che ci sembra plausibile sta nel fatto che le nostre immagini mentali di oggetti tridimensionali (come la botte, le ciotole, i cubi, i flaconi di shampoo…) sono spesso immagini statiche e bidimensionali, quasi “fotografie”. Facendo riferimento a queste immagini mentali “fotografiche”, implicitamente, senza accorgercene, perdiamo le informazioni sulla profondità e facciamo riferimento solo a misure di lunghezza o semmai di aree, ma non certo di volume.
Un buon modo per superare questo “ostacolo percettivo”, se così possiamo chiamarlo, è certamente quello di imparare come stanno le cose ed educare la nostra intuizione attraverso il ragionamento. Ma ci sembra di poter dire che tutto questo vada accompagnato da una educazione che passi anche attraverso i sensi, e non solo quello della vista! Tenere in mano i flaconi di shampoo e valutarne il peso può essere d’aiuto. Riempire la ciotola piccola e svuotarla in quella grande, ripetendo l’operazione finché essa non è piena, è un altro modo per educare la nostra intuizione spaziale attraverso i sensi. Esperienze come questa (ripresa nel video qui sotto) possono essere un valido aiuto da dare ai gruppi di ragazzi che dovessero non riuscire a risolvere il problema “I viaggi di Gulliver”.

Un’esperienza come quella illustrata nel video può aiutare gli alunni nella comprensione di questo nodo critico (ed effettivamente ha aiutato i ragazzi delle classi in cui l’abbiamo proposta). Ma il nodo critico rimane e non ci si può illudere che un’esperienza isolata, per quanto ben studiata e ben realizzata, possa essere risolutiva.
Piuttosto, sarà bene prevedere di tornare su questa questione più e più volte, in problemi apparentemente lontani l’uno dall’altro, formulati in modi diversi, che pongano l’accento ogni volta su un particolare diverso, pur rifacendosi tutti al legame che c’è tra il rapporto di similitudine e i rapporti tra le aree e i volumi di figure simili. In “I viaggi di Gulliver” si parte da una situazione fittizia, legata ad un mondo puramente fantastico, ma non mancano situazioni reali attraverso le quali stimolare l’attenzione dei ragazzi.

Metacognizione

L’apparenza (ingenua) inganna

Un insegnamento facilmente trasferibile in altri ambiti che i ragazzi possono trarre da questo problema è che l’apparenza inganna. Il nostro intuito, ciò che ci sembra di poter dire “a prima vista”, va sempre accompagnato dal ragionamento; le nostre stime immediate non sono sempre per forza sbagliate, ma non sono nemmeno per forza valide: meglio valutare per bene, prendendosi il tempo necessario e facendo tutte le considerazioni del caso.

Per contro, questo problema dà prova anche del fatto che l’intuizione può essere allenata. Se non abbiamo confidenza con i volumi, se non ci siamo mai posti problemi attorno alla capienza dei contenitori che usiamo, se non siamo abituati a confrontare volumi di oggetti concreti o di figure geometriche, la prima volta che proviamo a fare una stima è facile che prendiamo una gran cantonata. Ma, in questo come in tutti i campi dell’apprendimento, fare esercizio aiuta: l’intuizione e l’immaginazione e, in particolare, la capacità di stimare delle misure possono ampiamente essere allenate.

Un problema memorabile

Gli errori non devono mai farci paura: si dice che “chi non fa, non falla” (sottintendendo, in realtà, che se uno non sbaglia è perché non fa nulla), ma si potrebbe anche dire che chi non sbaglia, non impara.

In questo caso particolare crediamo che tanto più lontane dalla realtà saranno state le risposte iniziali dei ragazzi (ossia tanto più grandi saranno stati i loro errori), tanto più sarà facile che se ne ricordino, e che insieme ad essi si ricordino che il rapporto tra le aree e il rapporto tra i volumi non sono uguali al rapporto di similitudine ma, rispettivamente, al suo quadrato e al suo cubo.

Strategie risolutive diverse

Essendo il lenzuolo / tovagliolo un rettangolo, è facile che i ragazzi trovino la risposta alle domande che lo riguardano anche senza riflettere sul rapporto che esiste tra le aree di figure simili, oppure riflettendoci solo a posteriori.
Note le misure dei lati di un lenzuolo nel nostro mondo (2,50 m e 3 m), possiamo trovare quelle di un lenzuolo lillipuziano dividendo per 12 e ottenendo così 21 cm (circa) e 25 cm. E si può trovare la misura dell’area del lenzuolo lillipuziano moltiplicando tra loro le misure dei suoi lati, ottenendo così circa 21 cm × 25 cm = 525 cm².

Non è possibile procedere esattamente nello stesso modo per il calcolo del volume della botte, innanzitutto perché le misure lineari della botte non sono note, ma anche perché i ragazzi certo non conoscono una “formula” per il calcolo del volume della botte!
Ai gruppi di alunni che non dovessero trovare una strada per calcolare il volume della botte, l’insegnante potrebbe suggerire (prima di fornire la soluzione nella discussione finale) di riscrivere i calcoli fatti per l’area del lenzuolo, senza eseguire le divisioni, in modo tale da poter riflettere sul rapporto tra le aree dei lenzuoli, così:

A partire da questa scrittura i ragazzi potranno riconoscere che il rapporto tra le aree dei due lenzuoli (quello lillipuziano e quello del nostro mondo) è il quadrato del rapporto di similitudine. E qualche gruppo potrebbe anche, per analogia, capire da qui che il rapporto tra i volumi delle botti è il cubo del rapporto di similitudine.

Interessante, infine, è l’escamotage trovato da un’alunna di una classe alla quale è stato proposto questo problema durante il periodo di sospensione delle lezioni in presenza a causa dell’emergenza sanitaria legata alla diffusione della CoViD-19. Sostanzialmente ha trovato lo spigolo di un cubo equivalente a una botte lillipuziana, l’ha moltiplicato per 12 e poi ha trovato il volume di un cubo con questo nuovo spigolo, equivalente ad una botte del nostro mondo.

Sperimentazione

Questo problema è tra quelli proposti nella sperimentazione legata al corso MathUp “Problemi e approfondimenti” per la Scuola secondaria di primo grado nell’anno scolastico 2017 / 2018.

Materiale necessario

Potrebbe essere utile, ma non indispensabile, avere a disposizione due contenitori simili, per svuotare il contenuto del più piccolo in quello più grande e mostrare che il rapporto tra i volumi non coincide con il rapporto di similitudine, un po’ come si vede nel video inserito all’interno di questo articolo.
Non è necessario che il rapporto di similitudine sia 1:12, anzi: meglio che non lo sia, in modo da non fornire direttamente la risposta agli alunni (e, anche, da non dover svuotare 1728 volte il contenitore piccolo in quello grande!).

Potrebbe essere utile anche avere a disposizione tanti cubetti uguali (o tanti parallelepipedi uguali) con i quali costruire cubi (o parallelepipedi) più grandi,  con gli spigoli multipli di quelli del cubetto o parallelepipedo originale per uno steso fattore, per far toccare con mano agli alunni il fatto che il rapporto tra i volumi di cubi simili (o di parallelepipedi simili) è uguale al cubo del loro rapporto di similitudine.

Problema tratto da…

I viaggi di Gulliver è tra i Problemi per matematici in erba citati in Diario di bordo (Sofia Sabatti, edizioni mateinitaly, 2020), un testo nel quale alcuni dei problemi presentati in questo sito vengono contestualizzati all’interno di un anno scolastico vissuto da una classe terza della scuola secondaria di primo grado.

Problemi collegati

Nei commenti a questo problema abbiamo già elencato diverse situazioni dalle quali si potrebbe prendere spunto per costruire problemi collegati a I viaggi di Gulliver. Qui su Problemi per matematici in erba ne proponiamo due in particolare: I flaconi di shampoo e Un prisma stellare.