Il vostro amico Giuliano vi ha invitato alla sua festa di compleanno, con la condizione che dovete venire con un cappello a forma di cono, proprio come quelli dei gelati, ma capovolto, con la punta in su. Giuliano (che è un po’ strano…!) vi ha chiesto che il cappello sia proprio delle stesse misure di quello che avrà lui e, per rendervi il compito più difficile, non vi dice le misure del suo cono-cappello, ma vi dice soltanto che ci sta (giusto giusto) in una scatola a base quadrata, con il lato del quadrato di 20 cm, e l’altezza di 24 cm.
Voi avete obiettato, giustamente, che non capite perché il cappello debba essere esattamente di quelle misure (pochi hanno la testa così grossa come quella di Giuliano…!) e sarebbe quindi ragionevole che vi chiedesse soltanto che le misure fossero più o meno come quelle del suo. Invece Giuliano si è proprio impuntato e dice che durante la festa farà una gara: chi ha il cappello con le misure più vicine al suo avrà un bellissimo premio. I premi di casa sua sono famosi, quindi… vale la pena provarci!
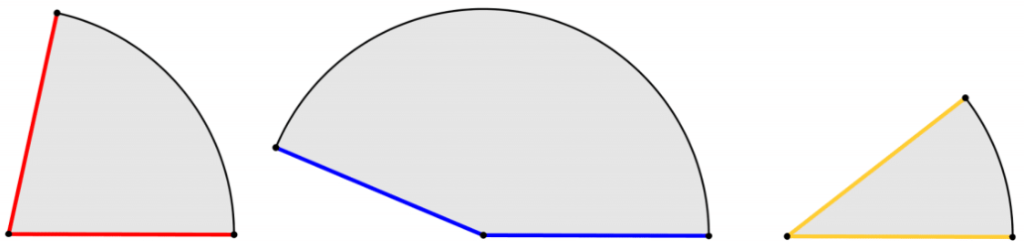
Forse già sapete, ma se non lo sapete ve lo diciamo noi, che, per costruire con il cartoncino un cono aperto, cioè senza il cerchio di base (proprio come quello dei gelati, per intendersi), si può utilizzare un settore circolare, che è una forma del tipo di quelle disegnate qui sotto (cioè la parte di cerchio compresa fra due raggi): se ritagliate una di queste forme e con un pezzo di scotch unite fra di loro i due raggi (a tratto più spesso in figura)… vi spunta fra le mani un cono.
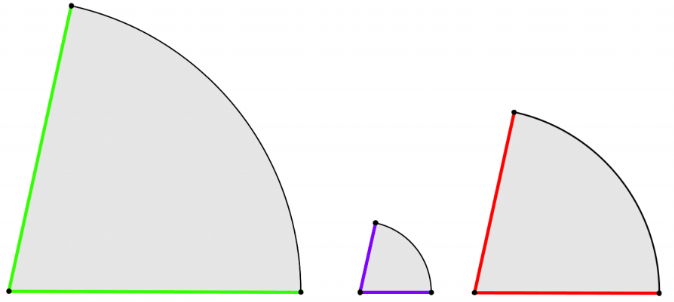
Per disegnare un settore circolare avete bisogno di due misure: la lunghezza del raggio del cerchio e l’angolo fra i due raggi. I tre settori circolari nella figura qui sopra sono ottenuti da tre cerchi dello stesso raggio (se controllate, vi accorgete che i segmenti colorati e più spessi hanno tutti la stessa lunghezza), ma cambia l’angolo fra i due raggi. Invece, i tre settori circolari nella figura qui sotto hanno tutti lo stesso angolo fra i due raggi, ma hanno i raggi di misure diverse.
Un consiglio: cominciate a fare un po’ di tentativi, registrando le vostre osservazioni, in modo da migliorare il tentativo successivo. Alcuni di voi potrebbero anche avere già studiato degli argomenti di matematica che vi possono aiutare in questo problema, ma… anche chi non li ha ancora studiati potrebbe vincere il premio di Giuliano!
Soluzione
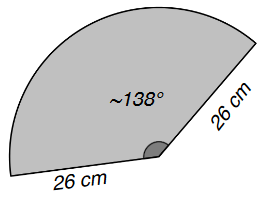
Il raggio del cerchio da cui estrarre il settore è di 26 cm e l’angolo tra i due raggi è di circa 138°. Naturalmente questa è solo una parte della soluzione: la soluzione completa (che per ovvi motivi non possiamo inserire qui!) consiste nella costruzione materiale di un cono di altezza 24 cm e diametro di base 20 cm.
Commenti
Un primo commento al testo del problema riguarda il richiamo ai coni-gelato, inserito per indurre i ragazzi a prendere in modo naturale il problema e a non irrigidirsi in una reazione del tipo: “ma noi non abbiamo ancora studiato i coni”.
L’idea è un po’ quella di prevenire una presa di posizione simile, con un taglio del tipo: “Non vi preoccupate, vi diciamo noi come sono fatti i coni: pensate a un gelato e andate avanti!”.
Per lo stesso motivo abbiamo evitato di usare nel testo la parola parallelepipedo e abbiamo parlato solo di una scatola.
Per permettere anche agli alunni più giovani di affrontare questo problema è importante intervenire in modo analogo anche di fronte a un eventuale “blocco” su un’altra parola (per esempio diametro o raggio, parole insomma che potrebbero essere già note ma potrebbero anche non esserlo).
La narrazione a proposito dell’amico che insiste per avere i cappelli proprio di quella dimensione nasce dal fatto che non sembra improbabile che, se venisse chiesto semplicemente di costruire un cappellino per una festa di compleanno, qualche ragazzino (o qualche gruppo) si accontenterebbe di una costruzione decisamente approssimativa, il che farebbe perdere la parte più significativa del problema.
Per insistere nella finzione, nel proporre il problema alla classe l’insegnante potrebbe davvero mettere in palio un premio per il gruppo il cui cono si avvicina di più alle misure richieste.
Questo problema ha l’obiettivo di far scontrare direttamente i ragazzi con le difficoltà (sia teoriche, sia pratiche) connesse al problema di realizzare un dato oggetto solido. In questo caso è proprio importante che i ragazzi possano pasticciare e sbagliare, perché solo se sbagliano, si accorgono di aver sbagliato, e poi si correggono possono veramente acquisire quello che vogliamo che acquisiscano con questo problema.
Nulla di male, quindi, se il primo tentativo è fatto con un settore un po’ a caso, con un angolo al centro assai lontano da quello corretto o con un raggio sbagliato (immaginiamo che molti possano scegliere come misura del raggio i 24 cm dell’altezza della scatola e quindi del cono).
L’importante è che, di fronte al primo tentativo, non ci si scoraggi, ma si misuri, si controlli, si capisca che non si è risposto al quesito e si cerchi di utilizzare la costruzione già fatta e gli errori già commessi per arrivare a un secondo (o terzo… o quarto…) tentativo che sia un po’ più corretto del precedente. Ci vorrà tempo, sicuramente; ma chi arriva in fondo se ne ricorderà. Mentre non è probabile che se ne ricordino se fornissimo loro soltanto delle istruzioni da seguire passo-passo per realizzare il cono con le misure corrette.
Magari faranno qualche tentativo errato, ma ci aspettiamo che prima o poi i ragazzi si rendano conto che le dimensioni della scatola danno loro (se il cono è contenuto “giusto-giusto”) il diametro di base e l’altezza del cono; a loro serve invece l’apotema, che corrisponde al raggio del settore.
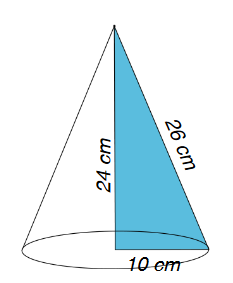
Coloro che già conoscono il teorema di Pitagora, potranno calcolare l’apotema del cono osservando che si tratta dell’ipotenusa di un triangolo rettangolo che ha un cateto di 24 cm e l’altro di 10 cm. Quindi l’apotema, ovvero il raggio del cerchio da cui estrarre il settore, è di 26 cm.
Procedendo per questa via, l’altra difficoltà con cui i ragazzi si devono scontrare è quella di determinare l’angolo al centro del settore circolare. Coloro che hanno già studiato le proprietà della circonferenza e le proporzioni potrebbero procedere in questo modo:
- osservare che l’arco di circonferenza corrispondente si attacca, nel cono, all’intera circonferenza di raggio 10 cm;
- ricavare che la lunghezza di questo arco è 20 π cm;
- osservare che l’intera circonferenza di raggio 26 cm ha lunghezza 52 π cm;
- ricavare che, di conseguenza, l’arco del settore che ci interessa è i 20/52, cioè i 5/13, dell’intera circonferenza.
Sicché l’angolo del settore circolare sarà i 5/13 di 360° cioè circa 138°.
È improbabile che i ragazzi facciano i conti in questo modo (lasciando indicata la lettera π, anziché moltiplicare per 3,14…); se però un gruppo si fosse accorto di questa possibilità, sarebbe proprio una bella scoperta, che sarà utile sottolineare come notevole a tutta la classe. E i ragazzi non mancheranno in questo caso di notare come si siano così risparmiati un bel po’ di conti…!
I ragazzi più giovani, che ancora non conoscono il teorema di Pitagora, le proporzioni e le proprietà della circonferenza, potranno “solo” procedere per tentativi ed errori, una via che peraltro non è esclusa anche per chi ha già anche altri strumenti, e una via che può essere, per gli uni e per gli altri, assai significativa.
Si presenta poi il problema di disegnare l’arco di circonferenza. Sia che i ragazzi abbiano fatto i calcoli e quindi cerchino di disegnare un settore avendo la misura del raggio e l’angolo compreso tra i due raggi, sia che invece stiano procedendo per tentativi e quindi abbiano l’obiettivo di disegnarne uno (per esempio) con il raggio un po’ più grande e l’angolo un po’ più piccolo rispetto al tentativo precedente, disegnare l’arco di circonferenza richiesto può non essere un problema facile.
Il raggio è grande, e quindi è improbabile che abbiano a disposizione un compasso di quella apertura. Lasciamo, anche qui, che si ingegnino! Hanno varie maniere per venirne a capo: possono per esempio disegnare (o stampare) su un foglio A4 e poi accostare tre copie di un settore circolare dello stesso raggio e di un angolo che sia 1/3 di quello di cui hanno bisogno. Oppure possono disegnare l’arco di circonferenza in maniera più artigianale usando una matita e una corda; lasciamoli fare, riservandoci solo la parte di chi li incoraggia e li incentiva sul fatto che vale la pena insistere: è possibile che ci stupiscano!
Non lasciamo soprattutto (e questo vale in particolare per i ragazzi più grandi) che le difficoltà matematiche si inseriscano a bloccare la realizzazione pratica. Se anche ai ragazzi più grandi non venisse in mente che basta applicare il teorema di Pitagora e calcolare il termine incognito in una proporzione per determinare raggio e angolo di quel settore, invitiamo anche loro a procedere per tentativi, come faremmo con i ragazzini più giovani, e facciamo loro capire che questo non è affatto male.
Procedere per tentativi in maniera il più possibile ragionata consolida nei ragazzi il concetto di misura e chiarisce loro (tramite un esempio pratico) che cosa vuol dire misurare, con tutte le difficoltà connesse alla approssimazione; inoltre, li conduce anche verso il concetto di funzione, perché devono osservare che cosa dipende da che cos’altro, quali sono i dati che hanno a disposizione in partenza e su cui possono intervenire (raggio e angolo del settore), quali sono i dati a cui vorrebbero arrivare (altezza e diametro di base del cono) e in quale maniera gli uni dipendono dagli altri.
Sperimentazione e possibili scenari
Un problema molto simile a questo, intitolato “Costruire un cono”, è stato sperimentato in 50 classi terze della scuola secondaria di primo grado durante il corso MathUp per la terza classe della scuola secondaria di primo grado nell’anno scolastico 2017 / 2018.
È stata proprio quella sperimentazione (e i commenti dei docenti che l’hanno portata avanti) che ci ha fatto pensare che il problema potesse utilmente essere proposto anche nelle classi prime e seconde, e anche con un diverso filo conduttore: non soltanto la geometria a tre dimensioni e la visualizzazione e costruzione di un oggetto solido (anche, senz’altro, per chi ha già certi strumenti), ma soprattutto le misurazioni, la capacità di utilizzare le misurazioni, queste uguaglianze che non sono proprio uguaglianze, ma solo “uguaglianze press’a poco”. Determinante in questo senso è stato il commento di una docente che raccontava, di fronte ai tentativi dei ragazzi, di essersi resa conto del fatto che
misurare è diverso da calcolare.
Il testo originale non prevedeva le figure attuali, ma solo un’altra figura, che qui sotto riportiamo, rappresentante un unico settore circolare.
Le figure attuali, e la spiegazione così articolata, sono pensate quindi soprattutto per permettere anche ad alunni che non abbiano ancora incontrato i settori circolari di affrontare questo problema. Non ci sembrano però inutili neanche per le altre classi: alcuni degli insegnanti che hanno proposto il problema “originale” nelle loro classi terze, infatti, avevano ritenuto “fuorviante” la figura con un unico settore circolare, perché alcuni alunni l’avevano interpretata come una rappresentazione non di un cono generico, ma del cono di cui si è alla ricerca. Altri insegnanti avevano già pensato ad una attività per facilitare la comprensione del problema da parte di tutti, nella stessa direzione che è stata seguita nel proporre le figure del testo attuale:
Il laboratorio potrebbe essere preceduto o seguito da un’attività di costruzione di settori circolari con lo stesso angolo al centro e diverso raggio, e di stesso raggio e diverso angolo al centro, per comprendere meglio ciò che succede (si ottengono coni più appuntiti o meno appuntiti? coni simili o coni non simili? sotto quali condizioni?)
In alcune delle classi terze che hanno partecipato alla sperimentazione MathUp, gli insegnanti hanno prima introdotto il cono, mostrando agli alunni un modellino di plastica trasparente oppure in cartoncino. Altri corsisti, invece, hanno usato il problema per introdurre l’argomento; in particolare un’insegnante scrive:
La didattica laboratoriale può anticipare l’apprendimento di nozioni e concetti formali, che non possono essere utili strumenti sin tanto che non si è compreso a che cosa servono. Se avessi per esempio proposto questo problema dopo aver già affrontato in classe lo studio del cono, forse avrei ottenuto risultati immediati e più soddisfacenti; invece il laboratorio mi ha offerto l’occasione per valutare l’effettivo apprendimento di alcuni concetti già visti in classe (relazioni tra le parti della circonferenza e del cerchio e calcolo delle loro misure) e per introdurre un argomento nuovo attraverso la scoperta.
Il problema, nella sua formulazione attuale, prescinde dal teorema di Pitagora, dalle proporzioni, e da qualunque nozione che i ragazzini delle classi prima o seconda della scuola secondaria di primo grado possono non avere ancora e chiede loro di procedere solo per tentativi ed errori: si tratta quindi di affinare la capacità di osservazione (per rendersi conto degli effetti che possono avere le diverse scelte che si operano sulla figura di partenza) e di misurare.
Materiale necessario
Sarà naturalmente necessario che i ragazzi abbiano a disposizione carta e cartoncino di dimensioni sufficientemente grandi, forbici e scotch. Ma anche compassi, cordini…
Ci immaginiamo che le risorse di carta e soprattutto di cartoncino non siano infinite, mentre sarebbe utile che i ragazzi avessero la possibilità di fare tutte le prove che ritengono necessarie.
Suggeriamo quindi intanto di riciclare materiale destinato alle discariche (cartoncino già utilizzato per altri lavori, giornali vecchi, …) e poi di fissare qualche “regola del gioco”. Per esempio se, come probabile, c’è abbondanza di carta ma non di cartoncino, si potrebbe riservare il cartoncino per un solo tentativo per ogni gruppo, quello finale, e usare la carta per gli altri.
Per alcune classi, o per alcuni gruppi, potrebbe essere utile lasciare a disposizione dei ragazzi anche qualche foglio con una fotocopia ingrandita delle sei figure presenti nel testo del problema e raccolte nel file allegato, in modo che comincino a fare qualche prova proprio con questi settori e osservino le caratteristiche dei coni così ottenuti.
Problema tratto da…
Questo problema è tra quelli proposti nella sperimentazione legata al corso MathUp “Problemi e approfondimenti” per la Scuola secondaria di primo grado nell’anno scolastico 2018 / 2019.
Problemi collegati
“I cappelli di Giuliano” è un problema che si presta bene ad essere presentato in maniera, oseremmo dire, teatrale. Il video seguente è un esempio di come si possa lanciare l’attività di risoluzione di questo problema in un modo alternativo alla consegna del testo scritto agli alunni.
Da questo problema, inoltre, si può prendere spunto per costruire altre attività. Ad esempio, l’insegnante che ha registrato il seguente video, dopo aver condotto gli alunni a riflettere sulle caratteristiche del cono e del settore circolare che costituisce lo sviluppo piano della sua superficie laterale, propone agli alunni due problemi, con testo molto più breve rispetto a quello de “I cappelli di Giuliano”, ma altrettanto significativi.



sei fantastica
grazie grazie grazie