Tag: geometria solida

Pubblicato il

Le confezioni della BestEraser

Per condividere con gli alunni il video che presenta questo problema, fornire il seguente link:
https://youtu.be/R5FFWDh5GoE

Domande e risposte

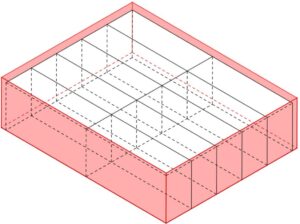
La gomma per cancellare descritta nel video-problema è un parallelepipedo i cui spigoli misurano 3,5 cm, 1,8 cm e 1,1 cm.
La ditta che produce queste gomme vuole imballarle in confezioni da dieci gomme ciascuna e sta valutando la possibilità di usare delle scatole già disponibili a magazzino: le scatole rosse (parallelepipedi di dimensioni 7,2 cm, 5,7 cm e 1,9 cm), le scatole blu (parallelepipedi di dimensioni 12 cm, 6,5 cm e 1,5 cm) o le scatole gialle (parallelepipedi di dimensioni 7,4 cm, 3,5 cm e 2,5 cm).
Ai ragazzi si chiede, in particolare, se c’è qualche scatola in cui si riescono a sistemare 10 gomme. Viene anche chiesto di descrivere il procedimento utilizzato per rispondere.

Per cominciare, si può calcolare il volume di una gomma e delle diverse scatole:

  • il volume di una gomma è 3,5 cm x 1,8 cm x 1,1 cm = 6,93 cm3 (quindi il volume di 10 gomme è 69,3 cm3);
  • il volume della scatola rossa è 7,2 cm x 5,7 cm x 1,9 cm = 77,976 cm3;
  • il volume della scatola blu è 12 cm x 6,5 cm x 1,5 cm = 117 cm3;
  • il volume della scatola gialla è 7,4 cm x 3,5 cm x 2,5 cm = 64,75 cm3.

In base a questi calcoli si può essere certi che la scatola gialla non riesce a contenere 10 gomme, dato che 64,75 < 69,3.

Non è però possibile, solo dal confronto dei volumi, stabilire molto altro. In particolare, il fatto che il volume della scatola rossa e quello della scatola blu siano maggiori del volume occupato da 10 gomme non basta per poter dire che queste scatole possano contenere 10 gomme, perché le gomme non sono un fluido che può essere versato nella confezione assumendone la forma!

La scatola rossa può contenere effettivamente 10 gomme: possiamo disporle in due file da 5 gomme ciascuna in modo che il lato da 1,8 cm della gomma sia in verticale (e possiamo farlo perché l’altezza della scatola è 1,9 cm e 1,8<1,9). Il fatto che 5×1,1<5,7 ci garantisce che lungo il lato da 5,7 cm ci stanno i lati da 1,1 cm di 5 gomme; il fatto che 2×3,5<7,2 ci garantisce che lungo il lato da 7,2 cm ci stanno i lati da 3,5 cm di 2 gomme.

Per quanto il volume della scatola blu sia ancora più grande di quello della scatola rossa, la scatola blu non può contenere 10 gomme. L’altezza della scatola (1,5 cm) infatti rende obbligatorio disporre le gomme in modo che il lato da 1,1 cm sia in verticale (gli altri lati della gomma infatti sono entrambi più lunghi di 1,5 cm). Con qualche tentativo, non è difficile rendersi conto che più di 9 gomme non possono essere inserite nella scatola blu.

Commenti

L’idea per Le confezioni della BestEraser è nata dalla discussione sorta tra alcuni insegnanti in merito a questo problema (tratto da un sussidiario per la scuola primaria):

In una cassa cubica con lo spigolo di 48 cm si mettono delle scatole che hanno il volume pari a 96 cm3 ciascuna. Quante scatole ci staranno?

Per alcuni degli insegnanti che hanno partecipato alla discussione, il problema così posto non poteva essere risolto, perché  nulla si dice sulla forma delle scatole; altri giungevano alla stessa conclusione, dando però per scontato che le scatole fossero dei parallelepipedi e lamentando il fatto di non conoscerne le dimensioni; altri ancora calcolavano il volume della cassa cubica (48 cm x 48 cm x 48 cm =  110592 cm3) e lo dividevano per il volume della singola scatola (110592 cm3 : 96 cm3 = 1152).
È bastato poco, tra colleghi, per trovare quale errore e quale “pregiudizio” si nascondesse sotto la sicurezza di chi sosteneva che nella cassa si potessero inserire 1152 scatole, indipendentemente dalla loro forma; è bastato chiudere gli occhi e cercare di immaginarsi la situazione, per capire che se le scatole da inserire sono sferiche o cilindriche, o hanno forme poliedriche ma bislacche, si “perde” un sacco di spazio. La discussione è proseguita poi per cercare di costruire per gli alunni un problema con un testo meno “perentorio”, che di per sé li invitasse a discutere e a non dare troppe cose per scontate.

Un problema significativo

Quanto raccontato nel video-problema non è un puro espediente, ma corrisponde a un problema reale, che si pone spesso a coloro che si occupano di attività produttive e commerciali: quello di impacchettare un certo numero di prodotti in una confezione oppure di ottimizzare la maniera di caricare in un camion un certo numero di scatole, magari anche di forme e dimensioni diverse.
I problemi di impacchettamento possono diventare davvero difficili, ma anche questo – nella sua relativa semplicità – è significativo perché fa capire come non sia sufficiente ragionare col volume degli oggetti e del contenitore in questione (nel nostro caso le gomme e le scatole), ma è necessario tenere conto della loro forma e dei differenti modi per disporre gli oggetti nel contenitore.

Se avessimo a che fare con fialette contenenti 6,93 cm3 di un certo liquido e volessimo riversare questo liquido in una bottiglietta della capacità di 117 cm3, basterebbe calcolare 117:6,93 per sapere che potremmo svuotare nella bottiglietta più di 16 ma meno di 17 fialette. Però se 6,93 cm3 è il volume di una gomma e 117 cm3 quello di una scatola, il risultato di questa divisione non ci dice molto.

Il volume ci dà effettivamente delle informazioni. E possono anche essere informazioni che tagliano la testa al toro in modo molto comodo: per esempio, è bastato calcolare il volume della scatolina gialla per dire che essa non può contenere 10 gomme (perché il suo volume è minore di quello di 10 gomme). In generale, il fatto che una scatola abbia il volume maggiore del volume di 10 gomme è una condizione necessaria affinché la scatola contenga 10 gomme.
Non è però una condizione sufficiente. Lo si può capire facilmente pensando ad una scatola anche dal volume enorme, con due dimensioni enormi, ma con la terza dimensione minore di 1 cm (e quindi più corta dello spigolo più piccolo della gomma, lungo 1,1 cm): in una scatola di questo tipo, per quanto il suo volume possa essere arbitrariamente grande, non si riesce a infilare nemmeno una gomma!

Da questa osservazione è possibile ricavare una condizione sufficiente (ma non necessaria) affinché si possano inserire 10 gomme in una scatola: se una delle dimensioni della scatola è (anche di poco) più grande di una delle dimensioni della gomma moltiplicata per 10, basta che ciascuna delle altre due dimensioni della scatola sia (anche di poco) più grande di una delle altre due dimensioni della gomma; in questo caso le gomme si potranno inserire nella scatola in una unica fila formata da 10 gomme.
Un’altra condizione sufficiente (ma, ancora, non necessaria) affinché si possano inserire 10 gomme in una scatola potrebbe essere questa: se una delle dimensioni della scatola è (anche di poco) più grande di una delle dimensioni della gomma moltiplicata per 5, e un’altra dimensione della scatola è (anche di poco) più grande del doppio di un’altra dimensione della gomma, basta che la terza dimensione della scatola sia (anche di poco) più grande della terza dimensione della gomma; in questo caso le gomme si potranno inserire nella scatola in due file sovrapposte formate da 5 gomme ciascuna.
Queste condizioni sono facili da verificare con i conti o con il righello (che misura lunghezze e non volumi!) come suggerito nel video, anche senza costruire in cartoncino 10 modellini di gomme: conti o righello possono essere utilizzati per controllare quante volte le dimensioni della gomma siano contenute in quelle delle scatoline, focalizzando l’attenzione sulle dimensioni lineari.
Chiaramente nessuna di queste due condizioni è necessaria, dal momento che non si richiede che tutte le gomme siano riposte “nello stesso modo” all’interno della scatola. Con questo intendiamo dire che, per quanto quelle di questo tipo siano le disposizioni con le quali ci viene più “naturale” fare i primi tentativi, non è detto che gli spigoli delle gomme di uguale lunghezza debbano essere tutti paralleli e quindi molte altre disposizioni sono possibili.

Strategie risolutive diverse

Possiamo prevedere, accettare e addirittura stimolare sia un approccio molto concreto a questo problema (quello di chi costruisce i modellini in cartoncino e va per tentativi) sia un approccio più astratto (quello di chi si mette a ragionare direttamente sulle misure).
Se in una classe gruppi di alunni diversi useranno diversi approcci, confrontarli durante la discussione finale sarà un arricchimento per tutti.

Potrebbero inoltre emergere modi diversi di sistemare lo stesso numero di gomme all’interno della stessa scatola. Anche questa molteplicità di proposte sarà da valorizzare: spesso abbiamo (e più noi adulti dei ragazzi…!) un modo di pensare molto rigido e stereotipato per cui, se siamo abituati a vedere la gomma appoggiata al tavolo in un certo modo, tendiamo a pensarla solo in quella posizione anche quando dobbiamo immaginare come riporla nella scatola. Se qualche gruppo non riuscisse a inserire 10 gomme nella scatola rossa, ciò potrebbe essere dovuto proprio al continuare a pensare alle gomme appoggiate al fondo della scatola sulla loro faccia “più estesa”:  vedere le 10 gomme inscatolate dai loro compagni potrà aiutarli  a superare questa rigidità.

Un problema aperto

Sono tante le domande che potrebbero nascere nei ragazzi, o che l’insegnante potrebbe porre loro per continuare a riflettere sui nodi proposti da questo problema o per verificarne l’effettiva comprensione. Ad esempio:

  • sapreste progettare altre scatole a forma di parallelepipedo, che contengano 10 gomme uguali a quelle descritte nel video-problema?
  • sapreste immaginare una scatola a forma di parallelepipedo, con un volume maggiore di quello di 10 gomme (cioè un volume maggiore di 69,3 cm3), dove però non si riesca a far stare nemmeno una gomma di quelle descritte nel video-problema?
  • sapreste immaginare una gomma, sempre a forma di parallelepipedo, sempre con un volume di 6,93 cm3 che però, anche da sola, non possa essere contenuta in alcuna delle tre scatole descritte nel video-problema?

Scenari possibili

Questo video-problema può essere tranquillamente proposto in una classe terza della scuola secondaria di primo grado.

Ma può essere proposto pure in una classe quinta della scuola primaria, anche senza dover dare a ciascun gruppo di lavoro le dieci gomme e le tre scatoline, a patto di averli fatti lavorare in precedenza su alcuni esempi concreti: quante risme di carta ci stanno nel cassetto della cattedra? Quante scatole di un certo tipo ci stanno nell’armadio della classe? Quanti volumi dell’enciclopedia ci stanno nello scaffale della libreria della biblioteca? Quanti pacchetti di fazzolettini di carta ci stanno nella scatola che la maestra ha portato per tenerli in classe?

Materiale necessario

Come già specificato, non è necessario che ogni gruppo di lavoro abbia a disposizione le tre scatole e le 10 gomme, anzi: il fatto di non averle (o di essere sufficientemente pigri per non aver voglia di costruirsene dei modelli in cartoncino) può spronare verso il ragionamento e l’astrazione.

È però importante che venga lasciata la possibilità a chi ne sente l’esigenza di costruirsi questi modelli in cartoncino, in modo da verificare le proprie ipotesi o da avere abbastanza elementi per formularne di nuove.

Un modello concreto costruito dall’insegnante, o le foto riportate in questo articolo, o alcuni disegni ben fatti possono essere d’aiuto per convincere alunni particolarmente scettici e particolarmente in difficoltà.

Problemi collegati

Tra i Problemi per matematici in erba ce n’è un altro, sempre legato a come alcuni parallelepipedi possano essere inscatolati in un parallelepipedo più grande: La fabbrica di saponette.
I due problemi, per quanto simili, offrono spunti di riflessione diversi e complementari.

Pubblicato il

Costruire un pallone da calcio


Per condividere con gli alunni il video che presenta questo problema, fornire il seguente link:
https://youtu.be/lNfwicOaAHs

Domande e risposte

A partire dal reticolo esagonale allegato a fondo pagina (citato nel video come “il disegno di Simone”) è possibile costruire un solido che ricorda un pallone da calcio.

Quante facce esagonali ha questo solido? E quante pentagonali?

Il solido che si ottiene nel video e che assomiglia a un pallone da calcio ha 20 facce esagonali e 12 “buchi” pentagonali, in corrispondenza di ciascuno dei quali possiamo immaginare una faccia.

Quanti esagoni ci sono nel reticolo del disegno di Simone?

Nel reticolo che appare sul disegno mostrato nel video si possono contare 39 esagoni, 8 dei quali vengono poi “eliminati” dai tagli lungo le linee continue.

Istruzioni

La richiesta di scrivere delle istruzioni precise, che consentano a chi non ha visto il video di ricostruire il solido, può essere soddisfatta in molti modi.

Dalle istruzioni deve emergere il fatto che alcuni esagoni vanno incollati su altri esagoni, lasciando dei “buchi” a forma di pentagono. Come suggerito nel video, indicare sullo stesso disegno quali esagoni vadano incollati su quali altri potrebbe facilitare di molto le cose.

In questo reticolo sono evidenziati con due colori diversi gli esagoni che vanno incollati su altri esagoni.
FIGURA 1 – In questo reticolo gli esagoni che rimangono dopo aver tagliato lungo le linee continue sono colorati in due modi diversi. Ogni esagono chiaro dovrà essere incollato a un esagono scuro. In particolare ogni esagono chiaro adiacente a uno scuro tramite una linea continua dovrà essere incollato proprio a quell’esagono scuro. Se si vuole che alla fine il solido abbia tutte le facce esagonali dello stesso colore (scure), si dovranno fare le pieghe “a monte” e si dovranno incollare gli esagoni chiari SOTTO gli esagoni scuri.
In questo reticolo gli esagoni da incollare uno sull'altro sono indicati con lo stesso numero.
FIGURA 2 – In questo reticolo ciascuno degli esagoni che rimangono dopo aver tagliato lungo le linee continue è etichettato con un numero o con un numero “bis”. L’esagono con l’etichetta n-bis deve essere incollato all’esagono con l’etichetta n. Si può osservare che quasi tutte le coppie di esagoni n e n-bis sono adiacenti lungo una linea continua; fanno eccezione le tre coppie 1 e 1bis, 19 e 19bis, 20 e 20bis.

Commenti

Un problema significativo

Immaginare a occhi chiusi, costruire a occhi aperti

Spesso, nella scuola, si parla della necessità di sviluppare le capacità di visualizzazione spaziale degli alunni. Particolarmente rilevante è, a questo proposito, la capacità di pensare il solido che si può costruire a partire da un certo sviluppo piano. Questa abilità può essere allenata attraverso varie esperienze concrete, purché sempre accompagnate da opportune riflessioni: costruire solidi a partire dal loro sviluppo piano; disegnare lo sviluppo piano di un solido dato; individuare sviluppi piani diversi dello stesso solido; indicare – su un dato sviluppo – quali lati dei poligoni che lo compongono andranno a combaciare con quali altri lati per costruire un certo solido…

In questo problema, le abilità di visualizzazione spaziale degli alunni entrano ancor più in gioco, insieme alla immaginazione, in quanto il reticolo esagonale disegnato sul foglio di carta NON coincide con lo sviluppo piano del solido: ci sono tanti esagoni di troppo e… mancano i pentagoni!

Dove si nascondono alcuni esagoni? Da dove vengono i pentagoni? Nello scrivere le istruzioni richieste, gli alunni dovranno, in un certo senso, rispondere a queste domande.
La situazione che si presenta più frequentemente è questa: 6 esagoni disposti ad anello attorno a un settimo esagono completamente delimitato da linee continue (e che quindi diventerà un buco nel reticolo); i 6 esagoni diventano 5 perché uno di essi viene incollato su un altro e l’esagono centrale diventa un buco pentagonale.

Ma ci sono anche coppie di esagoni che sul reticolo sono “lontani” e che devono essere incollati uno sull’altro: lo si capisce anche prima di aver costruito il solido, perché altrimenti non si potrebbe ottenere qualcosa che assomiglia a un pallone. Non è però facile capire di quali esagoni si tratti, se ci si limita a osservare il reticolo o a guardare il video! Dopo aver costruito il solido, però, attraverso un gioco di passaggi continui dalla manipolazione alla riflessione (e viceversa), dal pensare al toccare (e viceversa), dal costruire a occhi aperti all’immaginare a occhi chiusi (e viceversa) i ragazzi potranno concludere che gli esagoni “lontani” da incollare uno sull’altro saranno quelli indicati in FIGURA 2 con le etichette 1 e 1bis, 19 e 19bis, 20 e 20bis.

cogliere le analogie

Una buona dose di immaginazione serve anche per vedere l’analogia tra il pallone da calcio e l’oggetto, pieno di buchi, che si costruisce col cartoncino, nonché tra questo oggetto e il poliedro archimedeo con 20 facce esagonali e 12 facce pentagonali che è rappresentato nella figura qui sotto.

Comparison of truncated icosahedron and soccer ball

Un problema memorabile

Tanti fattori possono rendere questo problema memorabile: lo stupore che si prova nel vedere che da un reticolo fatto di soli esagoni nasce un solido in cui si individuano anche dei pentagoni, il fatto che si parli di un oggetto tanto comune quanto amato come il pallone da calcio, il fatto che i ragazzi si scoprano capaci di costruire da soli qualcosa di veramente bello…

Ciascun insegnante, nel contesto della propria classe, saprà agganciare a questo problema discussioni, riflessioni e scoperte in modo tale che tornino facilmente alla mente degli alunni, ogni volta che rivedranno o ripenseranno a un pallone da calcio!

Un problema aperto

In questo video-problema si chiede agli alunni di contare quanti sono gli esagoni e quanti sono i buchi pentagonali nell’oggetto che si costruisce a partire dal reticolo esagonale, che è come contare gli esagoni e i pentagoni che, una volta cuciti insieme, formano un pallone da calcio; ed è anche come contare le facce del poliedro che il pallone da calcio richiama.

È probabile che, mentre cercano di risolvere questo problema, gli alunni stessi si pongano ulteriori domande ed è utile che l’insegnante le raccolga, soprattutto se intende approfondire alcune questioni.

come si chiama il poliedro corrispondente al pallone da calcio?

È sorprendente la necessità (a volte quasi impellente) che i ragazzini hanno di dare un nome agli oggetti che imparano a riconoscere. E i nomi di questo poliedro possono far nascere altre domande.

Un nome attribuito a questo poliedro è icosaedro tronco (o troncato): perché?
Una risposta “visuale” (che, a seconda dell’età degli studenti, si potrà tradurre in modo sempre più appropriato nel linguaggio della geometria) si trova nel video qui sotto, tratto dal canale YouTube Mnogogranniki Ru (un canale educativo russo, tutto dedicato ai poliedri). Nel video si mostra come questo poliedro si ottiene a partire da un icosaedro “tagliando via”, intorno a ciascuno dei 12 vertici, una piramide (che sarà a base pentagonale, perché in ogni vertice arrivano 5 facce).

Qualcuno indica questo poliedro come poliedro uniforme (5, 6, 6): perché?
Si tratta di un poliedro uniforme perché intorno a ogni suo vertice arrivano gli stessi poligoni e, inoltre, comunque si fissino due vertici, è possibile rigirare il poliedro in modo da spostare il primo nella posizione del secondo. Queste caratteristiche fanno sì che il poliedro si possa identificare con una serie di numeri che indicano (in ordine) il numero di lati delle facce che arrivano in uno stesso vertice. Il nostro poliedro dunque è un poliedro uniforme di tipo (5,6,6): in ogni vertice arrivano un pentagono regolare e due esagoni regolari.

Un poliedro uniforme (5,6,6)

Quanti sono gli spigoli del poliedro corrispondente al pallone da calcio?

Questa domanda equivale a chiedersi quante sono le cuciture che bisogna fare per costruire il pallone da calcio a partire da pezze esagonali e pentagonali.
Per rispondere, gli alunni possono iniziare a contare spigolo per spigolo, magari aiutandosi con un pennarello per non rischiare di contare lo stesso spigolo due volte. Non è raro, però, che (pensando al pallone da calcio e alle pezze da cucire insieme) in qualche gruppo i ragazzi si accorgano che ogni cucitura unisce due lati, di due pezze diverse. I lati delle pezze esagonali sono 20×6=120; i lati delle pezze pentagonali sono 12×5=60; i lati sono quindi in tutto 180 e le cuciture da fare saranno 180:2=90.

Quanti sono i vertici del poliedro corrispondente al pallone da calcio? C’è qualche legame tra il numero delle facce, degli spigoli e dei vertici?

Contate le facce e contati gli spigoli, si possono contare (uno alla volta, o con qualche strategia che faccia riferimento alla simmetria del poliedro) anche i vertici.
A partire da questo e da altri problemi che abbiano a che fare con il numero di facce, vertici e spigoli di un poliedro, si potranno avvicinare gli alunni alla relazione di Eulero, dando così loro l’occasione di toccare un nodo della matematica profondo e importante, di cui parleremo nella sezione Quasi un libro.

Un problema difficile

La difficoltà di questo problema, inizialmente, potrebbe sembrare di tipo manuale. In realtà i ragazzi si accorgeranno presto che la costruzione di questo solido non è più complicata di quella di tanti altri che si possono fare con cartoncino, forbici e colla: la costruzione di molti solidi, anche se apparentemente più semplici, richiede infatti maggior precisione nei tagli (perché gli angoli delle facce o tra una faccia e l’altra sono più stretti) o nella fase di incollaggio (perché le superfici da incollare sono più sottili o difficili da stringere tra le dita).

La vera difficoltà sta nello scrivere delle istruzioni che servano a qualcuno che non ha potuto vedere il video: occorre osservare bene quanto viene proposto dall’insegnante, provare a ripeterlo (probabilmente più volte) focalizzando l’attenzione sui diversi passaggi che si compiono e trovare un modo per descriverli che sia davvero utile allo scopo. Entrano qui in gioco abilità e competenze linguistiche, perché i ragazzi dovranno fare un uso appropriato ed efficace del linguaggio; ma entrano in gioco anche abilità e competenze che hanno molto a che fare con la matematica e con il pensiero computazionale, per quanto non si vedano numeri, né calcoli, né calcolatori automatici!

Un problema di matematica con effetto sorpresa

Le sorprese suscitate da questo problema possono essere tante, a seconda della classe a cui lo proponiamo.

Chi non ha mai osservato da vicino un classico pallone da calcio e non ha mai notato le cuciture che caratterizzano la sua superficie risulta sorpreso nello scoprire che non si tratta di una sfera perfetta e uniforme, bensì del risultato di tanti singoli poligoni che si inarcano verso l’esterno per effetto della pressione dell’aria interna al pallone stesso.
Molti di quelli che, invece, queste cuciture le hanno già notate si stupiscono del fatto che i singoli pezzi non sono tutti esagoni, anche se con poco sforzo (pensando alla tassellazione del piano in esagoni che si può immaginare guardando i favi di un’arnia o i pavimenti di molte cucine…) si accorgono che, con esagoni soltanto, non si può fare una palla: tre esagoni regolari posti attorno a un unico vertice si uniscono uno all’altro formando una superficie piana.
Quasi tutti si stupiscono, a buon conto, che dal reticolo di soli esagoni si possa costruire il pallone da calcio: non è facile, all’inizio, immaginare che basti lasciare dei buchi pentagonali per ottenere l’effetto desiderato!

Scenari possibili

Questo problema si presta ad essere proposto a livelli molto diversi (meglio se adeguando il tono del racconto e delle richieste all’età dei nostri interlocutori).

Per alunni della scuola primaria, potrebbe essere il coronamento di una serie di attività sui poliedri o sulla geometria solida, mentre per alunni della scuola secondaria potrebbe essere usato come avvio allo studio dei poliedri (per il primo grado) e della relazione di Eulero (per il secondo grado).

Materiale necessario

A fondo pagina è possibile scaricare il file con il reticolo di cui si parla nel video-problema.

È opportuno dare a ogni alunno questo reticolo stampato su cartoncino (quello da 120 g/m2 è dello spessore adatto), in modo da poter costruire il proprio pallone da calcio. È altrettanto opportuno che ogni alunno, o ogni gruppo, riceva qualche copia in più, stampata anche solo su carta, per poterci lavorare al fine di scrivere le istruzioni richieste.

Allegati

Privacy Contatti Immagini Ringraziamenti e credits Licenza Proudly powered by WordPress
My Agile Privacy
✕
Questo sito utilizza cookie tecnici e di profilazione. Cliccando su accetta si autorizzano tutti i cookie di profilazione. Cliccando su rifiuta o la X si rifiutano tutti i cookie di profilazione. Cliccando su personalizza è possibile selezionare quali cookie di profilazione attivare.
AccettaRifiutaPersonalizza
Attenzione: alcune funzionalità di questa pagina potrebbero essere bloccate a seguito delle tue scelte privacy